gpu font rendering

GPUフォントレンダリング

これは、フォントで定義されたベクトルのアウトラインを使用して、GPUでテキストを直接レンダリングするデモです。

グリフの輪郭は、GPUにアップロードされる個々の2次皮肉な曲線（制御ポイントで定義）のリストに変換されます。

各グリフに対してクワッドが生成され、ピクセルシェーダーは各ピクセルがグリフの内側か外にあるかを決定します。これを行うために、ピクセルの巻線番号は、ベジエ曲線と光線を交差させることによって計算されます。すべての交差点で、光線は、光線に対するベジエ曲線の方向によって決定されるように、満たされた領域に入るか、出口に入ります。出口ごとに巻き上げ数は1つずつ増加し、すべてのエントリで巻線数が1つ減少します。すべての交差点を検討した後、ピクセルがアウトライン内にある場合、巻線数はゼロではありません。

光線の方向は、この巻き上げ数の計算では関係ありませんが、数学はX軸に平行な光線を使用することで大幅に簡素化できます。ベジエ曲線の制御ポイントからサンプル位置を差し引くことにより、座標系がシフトされ、光線の起源が $（0、0）$そして、光線は正のX軸と一致します。光線とbezier曲線の間の交差点のために条件 $ y = 0 $そして $ x ge 0 $その後、真実でなければなりません。アンチエイリアシング（以下を参照）は光線の方向に沿って発生しますが、最初に原点の周りのベジエ曲線の制御ポイントを回転させて、光線が再びX軸と整列するようにすることで他の方向を達成できます。

光線と単一のbezier曲線の間の交差点を見つけるには、次の式で二次bezier曲線が説明されていることを思い出してください（ベジエ曲線の背景については、美しさとプライマーを参照してください）：

$$ textbf {c}（t）=（1-t）^2 textbf {p} _0 + 2（1-t）t textbf {p} _1 + t^2 textbf {p} _2 $$

Y成分のみを採取し、条件を適用します $ y = 0 $単純な二次方程式になります：

$$（1-t）^2 textrm {y} _0 + 2（1-t）t textrm {y} _1 + t^2 textrm {y} _2 = 0 $$

次のように再配置できます。

$$ textrm {y} _0 -2t textrm {y} _0 + t^2 textrm {y} _0 + 2t textrm {y} _1-2t^2 textrm {y} _1 + t^2 textrm {y} _ 2pt

$$（ textrm {y} _0-2 textrm {y} _1 + textrm {y} _2）t^2-2（ textrm {y} _0- textrm {y} _1）t + textrm {y} {y} _0 = 0 $ $ $

2次式を使用して解決できるように：

$$ t_ {0/1} = {-b pm sqrt {b^2-4ac} over 2a} $$

$$ a = textrm {y} _0-2 textrm {y} _1 + textrm {y} _2 quad b = -2（ textrm {y} _0- textrm {y} _1） quad c = textrm {

代替 $ b = -2b $利回り：

$$ t_ {0/1} = { - （ - 2b） pm sqrt {（ - 2b）^2-4ac} over 2a} = {2b pm sqrt {4b^2-4ac} over 2a} = {b pm sqrt {b^2-ac}

$$ a = textrm {y} _0-2 textrm {y} _1 + textrm {y} _2 quad b = textrm {y} _0- textrm {y} _1 quad c = textrm {y} _0 $$

二次方程式にはゼロ、1つまたは2つのソリューションがあります。さらに、解決策 $ t $満足する必要があります $ 0 le t＆lt; 1 $制御ポイントによって記述されたセグメントにあること（エンドポイントは、アウトラインの次のセグメントの一部であるため除外されます）。最後に、解決策が与えられました $ t $対応するX座標は、として計算できます $ mathbf {c} _x（t）$ 2番目の条件を確認します $ x ge 0 $交差点のために。

この時点で、光線とbezier曲線の間の交差点が特定されていますが、それらはまだエントリまたは出口として分類する必要があります。 Dobbieによって提供されたデモは、それぞれのベジエ曲線の導関数を明示的に計算します $ t $これを行う価値。ただし、デリバティブは、両方の潜在的なソリューションについて一般的に計算することもできます $ t_0/t_1 $ ：

$$ mathbf {c} _y（t）=（ textrm {y} _0-2 textrm {y} _1 + textrm {y} _2）t^2-2（ textrm {y} _0 - textrm {y} _1）textre $$

$$ mathbf {c} _y（t）= at^2-2b t + c $$

$$ frac {d mathbf {c} _y（t）} {dt} = 2at -2b $$

$$ frac {d mathbf {c} _y（t_0）} {dt} = 2a {b- sqrt {b^2 -ac} over a} -2b -2 sqrt {b^2 -ac} -2b = -2 sqrt {b^2ac}

$$ frac {d mathbf {c} _y（t_1）} {dt} = 2a {b + sqrt {b^2-ac} over a} -2b + 2 sqrt {b^2-ac} -2b = 2 sqrt {b^2-ac

したがって、bezier曲線は、各溶液で固定方向にx軸を通過し、輪郭の方向性のための慣習と組み合わせて、 $ t_0 $常に出口です $ t_1 $常にエントリです。

この関係を理解するための別のアプローチは、ソリューションで使用されている異なる兆候と平方根が非陰性であるため、気付くことです。 $ t_0 $曲線に沿って最初に来なければなりません $（t_0＆lt; = t_1）$もし $ a＆gt; 0 $ 。逆に、if $ a＆lt; 0 $ 、次に、順序が逆になります $ t_1 $最初に来なければなりません $（t_1＆lt; = t_0）$ 。パラメーター $ a $として書き直すことができます $ 2（ frac { textrm {y} _0 + textrm {y} _2} {2} - textrm {y} _1）$ 、したがって、その符号は、2番目の制御ポイントが最初と3番目の制御ポイントの中間点の上または下にあるかどうかに依存します。次の図は、曲線の方向とパラメーターの符号のすべての組み合わせに対して、ソリューションが常に正しく分類されていることを示しています $ a $ 。曲線に沿った溶液の順序がどのように変化するかに注意してくださいが、光線は常に $ t_1 $解決策とaでの出口 $ t_0 $解決。

パラメーターの場合 $ a $ 0です（または浮動小数点計算では十分に小さい）、間に線形関係があります $ t $そして $ y $ （これは線形セグメントにも当てはまりますが、一部の非線形曲線にも当てはまります）。 $ a $ 。ただし、関係は線形になっているため、最大で1つのソリューションがあり、簡単に計算および分類されます。

光線方向に沿ったアンチエイリアスは、ウィンドウを光線起源の周りのピクセルのサイズのサイズと見なすことにより実装されます。交差点がこのウィンドウに落ちた場合、巻線数はわずかに変更され、ピクセルのカバレッジを計算します。分数重量は、ピクセルの左端からの距離によって決定されます（これは、右を指す光線と一致しています）。個々のセクションを考慮することにより、これが1次元のカバレッジを正確に計算することがわかります。

また、現在は光線起源の少し後ろに交差点を考慮する必要がありますが、実装では最初にx軸との交差点を計算し、次にXポジションを検証するため、あまり変化しません。これについての別の考え方は、その状態が $ x ge 0 $ 0の重み関数を意味します $ x＆lt; 0 $と1の $ x ge 0 $ 。 1ピクセルの幅に線形セグメントを導入することにより、不連続性を削除できます。

完全なアンチエイリアシングの場合、異なる方向に沿って複数の光線を使用できます（例：x軸に沿った1つ、y軸に沿って1つ）。

メモ

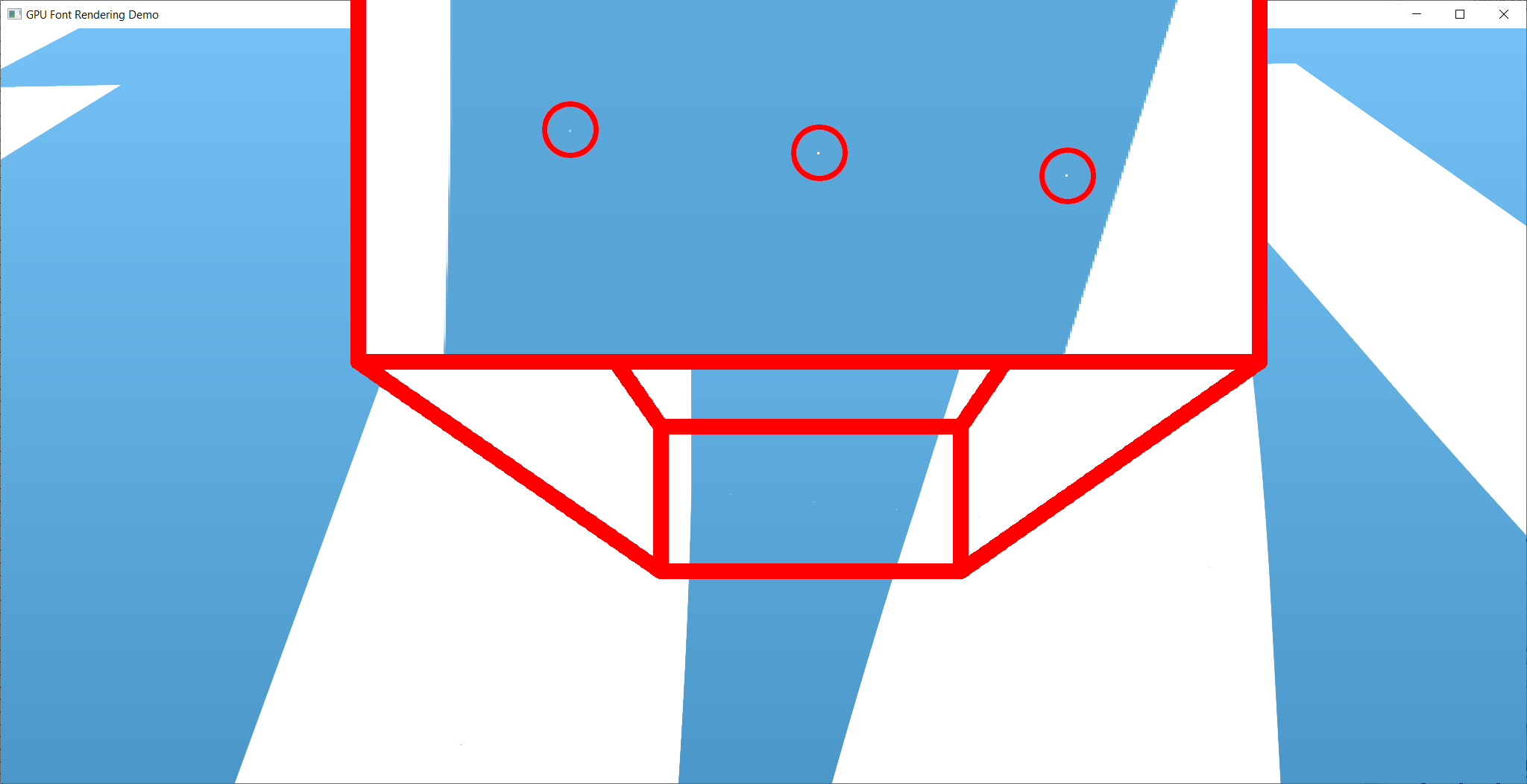
この種の手法は、浮動小数点数の限られた数値精度からのアーティファクトの対象となります。以下の画像は、完全にズームインしたとき（そしてどこを見るべきかを知っている）ときのそのようなアーティファクトのインスタンスを示しています。それにもかかわらず、私はこの実装がすでに非常に数値的に安定していることを発見しました。残りのアーティファクトは、関連する特許のためにここでは実装されていないSlugアルゴリズムを使用して排除できます。

また、このデモは、パフォーマンスの最適化（バンドなど）を実装せず、いくつかのシナリオや非常に複雑なフォントを使用する場合、GPUの使用量が高い場合があります。

指示を作成します

1. initサブモジュール

プロジェクトを再帰的にクローンして、依存関係のサブモジュールを初期化します（またはgit submodule update --init既にリポジトリをクローニングしている場合はInit）：

 git clone --recursive https://github.com/GreenLightning/gpu-font-rendering.git
cd gpu-font-rendering

2。CMAKEを使用します

 # Note: CMake will create the build directory.
cmake -S . -B build
make -j8 --directory build

Windowsでは、代わりにCmake GUIやVisual Studioを使用することをお勧めします。

Linuxでは、OpenGL開発のために追加のパッケージをインストールする必要がある場合があります（例えば、ubuntu用のsudo apt-get install xorg-dev libgl1-mesa-dev ）。

3.メインプロジェクトディレクトリから実行します

 ./build/main

このプログラムでは、リソースをロードするために、 fontsとshadersディレクトリが現在のディレクトリにあることを要求しています。あなたが黒い窓を手に入れた場合、これはおそらく問題です。作業ディレクトリを確認し、エラーがないかコンソールを確認してください。

Windows 10、Macos Monterey、Ubuntu 22.04でテストしました。