GPU字体渲染
这是使用字体定义的向量大纲直接在GPU上渲染文本的演示。
字形的轮廓转换为单个二次曲线曲线的列表(由其控制点定义),这些曲线已上传到GPU。
为每个字形生成四边形,然后像素着色器确定每个像素是内部还是外面的。为此,像素的绕组数是通过将射线与Bezzier曲线相交的。在每个交叉路口,射线要么进入或退出填充区域。在每个出口处,绕组数量都会增加一个,在每个入口时,绕组数量都会减少一个。考虑所有交叉点后,如果像素在轮廓内部,则绕组数将非零。
对于此绕组数量计算,射线的方向并不重要,但是通过使用与X轴平行的光线,可以大大简化数学。通过从bezier曲线的控制点减去样品位置,坐标系被移动,以使射线的起源在 $(0,0)$射线与正x轴一致。对于射线和偏斜曲线之间的交点 $ y = 0 $和 $ x ge 0 $必须是真实的。反叠缩(见下文)将沿射线的方向发生,但是可以通过首先旋转围绕原点的Bezier曲线的控制点来实现其他方向,从而使光线再次与X轴对准。
为了找到射线和单个bezier曲线之间的相交,请回想一下以下公式描述了二次曲线曲线(有关Bezier曲线的背景,请参见Beauty and Primer):
$$ textbf {c}(t)=(1-t)^2 textbf {p} _0 + 2(1-t)t textbf {p} _1 + t^2 textbf {p textbf {p} _2 $$
仅服用Y组件并应用条件 $ y = 0 $产生一个简单的二次方程:
$$(1-t)^2 textrm {y} _0 + 2(1-t)t textrm {y} _1 + t^2 textrm {y} _2 = 0 $$
可以重新排列:
$$ textrm {y} _0 -2T textrm {y} _0 + t^2 textrm {y} _0 + 2t + 2t 2t textrm {y} _1-2T^2 2t^2 textrm {y}
$$( textrm {y} _0-2 2 textrm {y} _1 + \ textrm {y} _2)
因此,可以使用二次公式来解决它:
$$ t_ {0/1} = {-b pm sqrt {b^2-4Ac} vose 2a} $$
$$ a = textrm {y} _0-2 2 textrm {y} _1 + \ textrm {y} _2 _2 quad b = -2( textrm {y} _0 - textrm {y} _1)
替代 $ b = -2B $产量:
$ t t_ {0/1} = { - ( - 2B) pm sqrt {( - 2b)^2-4ac} over 2a} = {2b pm sqrt {4B^2-4AC} acta
$$ a = textrm {y} _0-2 2 textrm {y} _1 + textrm {y} _2 quad b = textrm {y} _0 - textrm {y} _1 quad C = textrm
二次方程可能具有一个或两个解决方案。此外,一种解决方案 $ t $必须满足 $ 0 le t< 1 $要在控制点描述的段上(不包括终点,因为它是轮廓下一个段的一部分)。最后,给定解决方案 $ t $相应的X坐标可以计算为 $ mathbf {c} _x(t)$检查第二条件 $ x ge 0 $与十字路口。
在这一点上,已经确定了射线和Bezier曲线之间的相互作用,但仍需要将其分类为入口或退出。 Dobbie提供的演示明确计算了每个曲线的衍生物 $ t $这样做的价值。但是,对于两种潜在解 $ T_0/T_1 $ :
$ mathbf {c} _y(t)=( textrm {y} _0-2 2 textrm {y} _1 + textrm {y} _2 _2)t^2-2( textrm {y}
$$ mathbf {c} _y(t)= at^2-2b t + c $$
$$ frac {d mathbf {c} _y(t)} {dt} = 2at -2b $$
$ frac {d mathbf {c} _y(t_0)} {dt} = 2a {b - sqrt {b^2-ac} a}} - 2b = 2b = 2b -2b -2b -2 sqrt {b^2-ac} {b^2-ac} - 2-2-2-2-2-2-2-2-2-2-2-2-2-2b = -2 $ 0 0 $ 0 0 $ 0
$ frac {d mathbf {c} _y(t_1)} {dt} = 2a {b + sqrt {b^2-ac} a}} - 2b = 2b = 2b = 2b + 2 2 sqrt {b^2-ac} {b^2-ac} - 2-ac} - 2-ac} - 2b = 2 $}
因此,Bezier曲线在每个溶液处沿固定方向越过X轴,并与轮廓方向的惯例相结合, $ T_0 $永远是出口 $ T_1 $总是条目。
理解这种关系的一种不同的方法是注意,由于解决方案中使用的不同符号,而平方根是非负的,所以 $ T_0 $必须先沿着曲线 $(t_0< = t_1)$如果 $ a> 0 $ 。相反,如果 $ a< 0 $ ,然后订单被颠倒,然后 $ T_1 $必须先来 $(t_1< = t_0)$ 。参数 $ a $可以重写为 $ 2( frac { textrm {y} _0 + textrm {y} _2}} {2} {2} - textrm {y} _1)$ ,因此其符号取决于第二个控制点是第一个控制点和第三个控制点的中点以上还是低于中点。下图显示,对于曲线方向的所有组合和参数的符号,该解决方案始终正确分类 $ a $ 。请注意沿曲线的解决方案的顺序如何变化,但是射线总是进入 $ T_1 $解决方案并退出 $ T_0 $解决方案。
如果参数 $ a $是0(在浮点计算中足够小),之间存在线性关系 $ t $和 $ y $ (这对于线性段是正确的,但对于某些非线性曲线也是如此),由于通过 $ a $ 。但是,由于关系现在是线性的,因此最多可以有一个解决方案,该解决方案很容易计算和分类。
沿射线方向进行抗氧化剂是通过考虑射线原点周围像素大小的窗口来实现的。如果一个相交掉入此窗口,则仅分一分更改绕组数以计算像素的覆盖范围。分数重量取决于距像素左边缘的距离(这与指向右侧的射线是一致的)。通过考虑各个部分,可以看到这可以准确地计算一维覆盖范围。
请注意,我们还必须考虑现在稍后稍后稍后的射线源,但是该实现首先计算与X轴的任何交集,然后验证X位置,因此它不会发生太大变化。对此的另一种思考方式是条件 $ x ge 0 $表示为0的加权功能 $ x< 0 $和1 $ x ge 0 $ 。我们可以通过在一个像素的宽度上引入线性段来消除不连续性。
为了进行全面的抗氧化,我们可以沿着不同方向使用多个射线(例如沿X轴,沿Y轴沿X轴一个)。
笔记
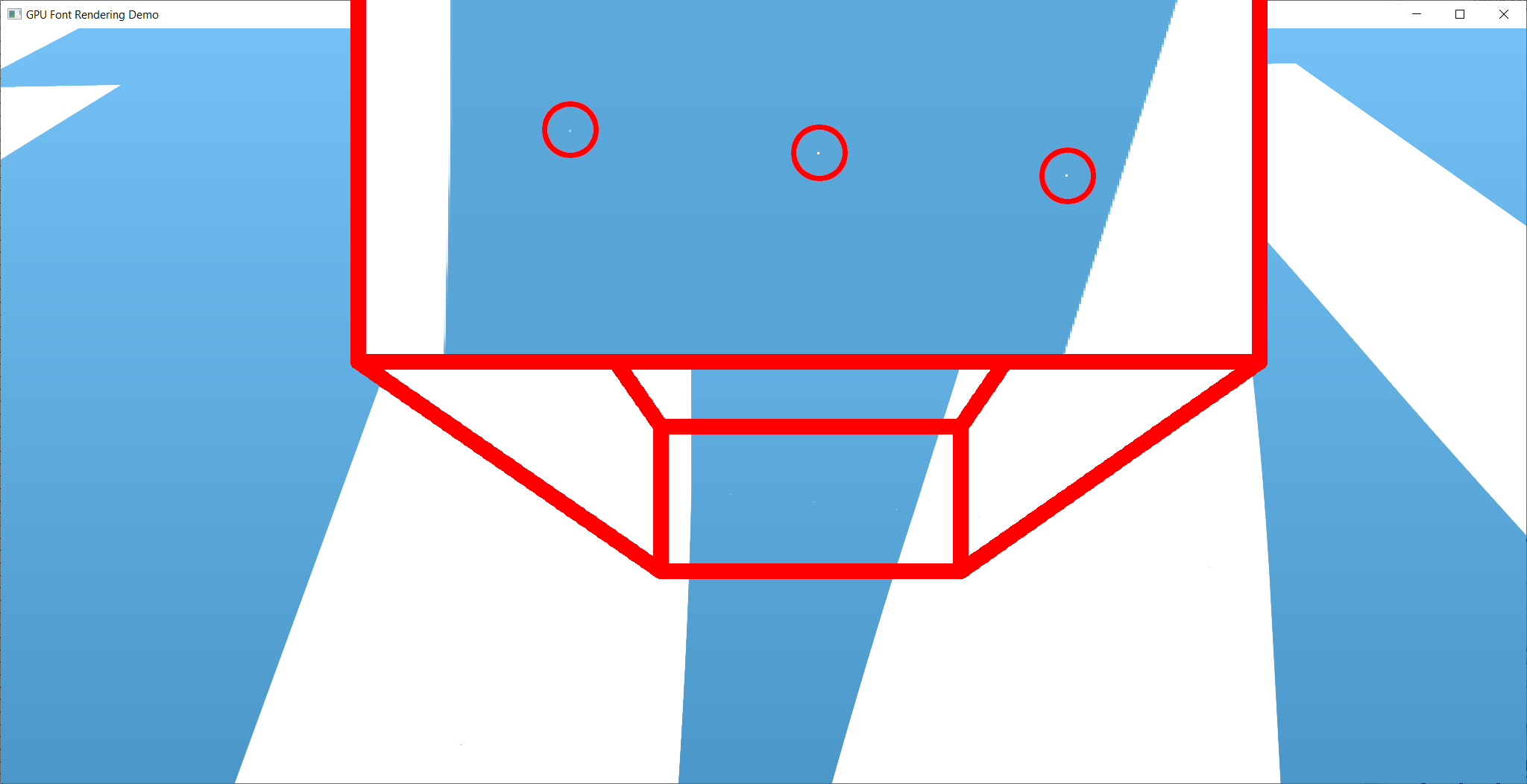
这种技术受到浮点数数量有限的数值精度的伪像。下图显示了完全放大(并知道在哪里看)时的此类工件的实例。但是,我发现此实现已经在数字上已经非常稳定了。可以使用SLUG算法消除剩余的任何伪像,由于相关专利,此处未实施。
该演示也不会实现任何性能优化(例如频段),并且在某些情况下以及使用非常复杂的字体时可能具有较高的GPU使用情况。
建立说明
1。初始化sodules
将项目递归克隆,以初始化依赖项的子模型(或运行git submodule update --init如果您已经克隆了仓库,请):
git clone --recursive https://github.com/GreenLightning/gpu-font-rendering.git
cd gpu-font-rendering
2。使用cmake
# Note: CMake will create the build directory.
cmake -S . -B build
make -j8 --directory build
在Windows上,您可能需要使用Cmake GUI和/或Visual Studio。
在Linux上,您可能必须安装其他软件包才能开发(例如,ubuntu sudo apt-get install xorg-dev libgl1-mesa-dev )。
3。从主要项目目录运行
该程序要求fonts和shaders目录在当前目录中以加载其资源。如果您只得到黑色窗口,那么这很可能是问题。检查您的工作目录并检查控制台是否错误。
在Windows 10,Macos Monterey和Ubuntu 22.04上进行了测试。
