gpu font rendering

GPU 글꼴 렌더링

이것은 글꼴로 정의 된 벡터 윤곽선을 사용하여 GPU에서 직접 텍스트를 렌더링하는 데 드는 데모입니다.

글리프의 윤곽은 GPU에 업로드되는 개별 2 차 베 지어 곡선 목록 (제어점에 의해 정의 됨)으로 변환됩니다.

각 글리프에 대해 쿼드가 생성되고 픽셀 셰이더는 각 픽셀이 글리프 내부 또는 외부에 있는지 여부를 결정합니다. 이를 위해, 픽셀의 와인딩 번호는 광선을 Bezier 곡선과 교차시켜 계산됩니다. 모든 교차로에서 광선은 광선에 대한 베 지어 곡선의 방향에 의해 결정된 바와 같이 충전 된 영역으로 들어가거나 나옵니다. 모든 출구에서 와인딩 번호는 1 씩 증가하고 모든 항목에서 와인딩 번호는 1 씩 줄어 듭니다. 모든 교차로를 고려한 후 픽셀이 개요 안에 있으면 와인딩 번호가 0이됩니다.

광선의 방향은이 와인딩 번호 계산에 중요하지 않지만 X 축과 평행 한 광선을 사용하여 수학을 크게 단순화 할 수 있습니다. Bezier 곡선의 제어점에서 샘플 위치를 빼면 좌표계가 광선의 기원이 $ (0, 0) $ 광선은 양의 x 축과 일치합니다. 광선과 베 지어 곡선 사이의 교차로 조건 $ y = 0 $ 그리고 $ x ge 0 $ 그런 다음 사실이어야합니다. 반 알리 아싱 (아래 참조)은 광선의 방향을 따라 발생하지만, 먼 방향은 먼저 원점 주위의 베 지어 곡선의 제어점을 회전시켜 x 축과 다시 일치하도록하여 달성 할 수 있습니다.

광선과 단일 Bezier 곡선 사이의 교차점을 찾으려면 2 차 베 지어 곡선이 다음 공식으로 설명되어 있음을 기억하십시오 (Bezier 곡선의 배경은 Beauty and Primer 참조).

$$ textbf {c} (t) = (1-t)^2 textbf {p} _0 + 2 (1-t) t textbf {p} _1 + t^2 textbf {p} _2 $$

y 성분 만 복용하고 조건을 적용합니다 $ y = 0 $ 간단한 2 차 방정식을 나타냅니다.

$$ (1-t)^2 textrm {y} _0 + 2 (1-t) t textrm {y} _1 + t^2 textrm {y} _2 = 0 $$

다음으로 재 배열 될 수 있습니다.

$$ textrm {y} _0 -2t textrm {y} _0 + t^2 textrm {y} _0 + 2t textrm {y} _1 -2T^2 textrm {y} _1 + t^2 textrm {y} _2 = 0 $ $

$$ ( textrm {y} _0 -2 textrm {y} _1 + textrm {y} _2) t^2-2 ( textrm {y} _0 - textrm {y} _1) t + textrm {y} _0 = 0 $$

2 차 공식을 사용하여 해결할 수 있도록 :

$$ t_ {0/1} = {-b pm sqrt {b^2-4ac} Over 2a} $$

$$ a = textrm {y} _0 -2 textrm {y} _1 + textrm {y} _2 quad b = -2 ( textrm {y} _0 - textrm {y} quad c = textrm {y} _0 $$

대체 $ b = -2b $ 수확량 :

$$ t_ {0/1} = {-(-2B) pm sqrt {(-2b)^2-4ac} Over 2a} = {2b pm sqrt {4b^2-4Ac} Over 2a} = {b pm sqrt {b^2-Ac}

$$ a = textrm {y} _0 -2 textrm {y} _1 + textrm {y} _2 quad b = textrm {y} _0- textrm {y} _1 quad c = textrm {y} _0 $$

2 차 방정식은 0, 하나 또는 두 개의 솔루션을 가질 수 있습니다. 또한 솔루션 $ t $ 만족해야합니다 $ 0 le t & lt; 1 $ 제어점에 의해 기술 된 세그먼트에 있으려면 (종점은 다음 개요의 다음 세그먼트의 일부이므로 제외된다). 마지막으로, 해결책이 주어졌습니다 $ t $ 해당 X- 코디네이트는 다음과 같이 계산할 수 있습니다 $ mathbf {c} _x (t) $ 두 번째 조건을 확인합니다 $ x ge 0 $ 교차로.

이 시점에서 광선과 베 지어 곡선 사이의 교차점이 식별되었지만 여전히 진입 또는 출구로 분류되어야합니다. Dobbie가 제공하는 데모는 각각에 대한 Bezier 곡선의 미분을 명시 적으로 계산합니다. $ t $ 이를위한 가치. 그러나 파생물은 일반적으로 잠재적 인 솔루션 모두에 대해 계산할 수 있습니다. $ t_0/t_1 $ :

$$ mathbf {c} _y (t) = ( textrm {y} _0 -2 textrm {y} _1 + textrm {y} _2) t^2-2 ( textrm {y} _0 - textrm {y} _1) t + textrm {y}}

$$ mathbf {c} _y (t) = at^2-2B t + c $$

$$ frac {d mathbf {c} _y (t)} {dt} = 2at -2b $$

$$ frac {d mathbf {c} _y (t_0)} {dt} = 2a {b- sqrt {b^2 -ac} a} -2b = 2b -2 sqrt {b^2 -ac} -2B = -2 sqrt {b^2 -aC}

$$ frac {d mathbf {c} _y (t_1)}} {dt} = 2a {b + sqrt {b^2-ac} a} -2B = 2B + 2 sqrt {b^2-ac} -2B = 2 sqrt {b^2-aC}

따라서 Bezier 곡선은 각 솔루션에서 고정 방향으로 X 축을 가로 지르며 윤곽의 방향을위한 규칙과 결합합니다. $ t_0 $ 항상 출구입니다 $ t_1 $ 항상 항목입니다.

이 관계를 이해하기위한 다른 접근법은 솔루션에 사용 된 다른 징후와 제곱근이 무분별하지 않기 때문에, $ t_0 $ 곡선을 따라 먼저 와야합니다 $ (t_0 & lt; = t_1) $ 만약에 $ a & gt; 0 $ . 반대로, if $ a & lt; 0 $ , 그러면 주문이 반전되고 $ t_1 $ 먼저 와야합니다 $ (t_1 & lt; = t_0) $ . 매개 변수 $ a $ 다시 작성할 수 있습니다 $ 2 ( frac { textrm {y} _0 + textrm {y} _2} {2} - textrm {y} _1) $ 따라서 부호는 제 2 제어점이 제 1 및 세 번째 제어 지점의 중간 점보다 높거나 아래에 있는지 여부에 따라 다릅니다. 다음 그림은 솔루션이 곡선 방향의 모든 조합과 매개 변수 부호에 대해 항상 올바르게 분류되어 있음을 보여줍니다. $ a $ . 곡선을 따르는 솔루션의 순서가 어떻게 변하는 지 주목하지만 Ray는 항상 $ t_1 $ 해결책 및 종료 a $ t_0 $ 해결책.

매개 변수 인 경우 $ a $ 0 (또는 부동 소수점 계산에서 충분히 작음). $ t $ 그리고 $ y $ (이것은 선형 세그먼트뿐만 아니라 일부 비선형 곡선의 경우에도 마찬가지입니다). $ a $ . 그러나 관계는 이제 선형이기 때문에 최대 하나의 솔루션이있을 수 있으며,이 솔루션은 쉽게 계산되고 분류됩니다.

광선 방향을 따르는 반 알리 아스는 광선 원점 주변의 픽셀 크기의 창을 고려하여 구현됩니다. 교차로 가이 창으로 떨어지면, 픽셀의 적용 범위를 계산하기 위해 교차로가 분수로 만 변경됩니다. 분수 중량은 픽셀의 왼쪽 가장자리로부터의 거리에 의해 결정된다 (이것은 오른쪽을 가리키는 광선과 일치한다). 개별 섹션을 고려함으로써, 이것은 1 차원 적용 범위를 정확하게 계산한다는 것을 알 수 있습니다.

우리는 또한 현재 광선 원점보다 약간 뒤에서 교차로를 고려해야하지만, 구현은 먼저 x 축과의 교차로를 계산 한 다음 x-position을 검증하므로 크게 변하지 않습니다. 이것에 대해 생각하는 다른 방법은 $ x ge 0 $ 0에 대한 가중치 기능을 의미합니다 $ x & lt; 0 $ 그리고 1 용 $ x ge 0 $ . 하나의 픽셀 너비에 선형 세그먼트를 도입하여 불연속성을 제거 할 수 있습니다.

완전한 반 알리어스를 위해 우리는 다른 방향 (예 : x 축을 따라 하나, y 축을 따라 하나)을 따라 여러 개의 광선을 사용할 수 있습니다.

메모

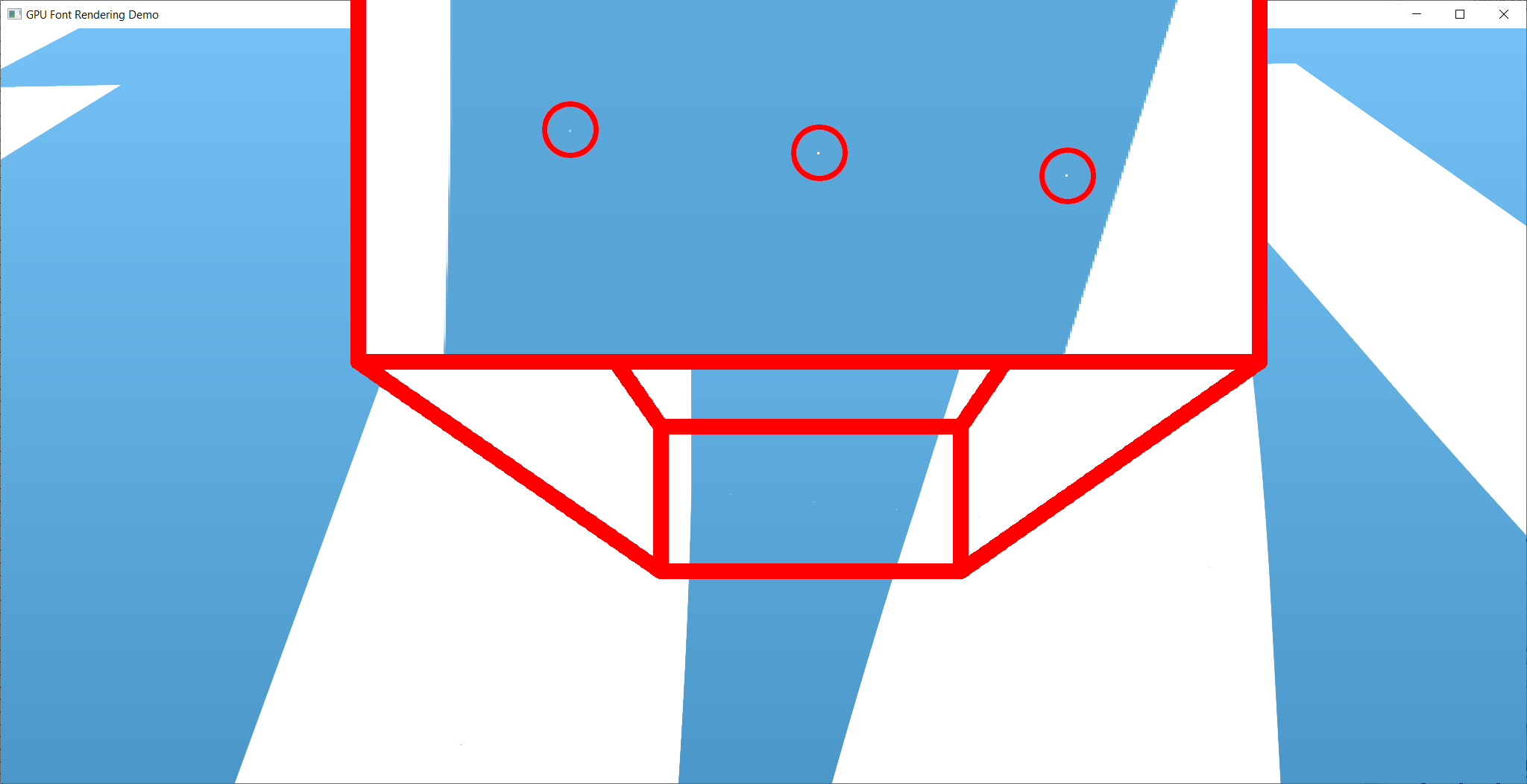
이러한 종류의 기술은 부동 소수점 수의 제한된 수치 정밀도로부터 인공물이 적용됩니다. 아래 이미지는 완전히 확대 될 때 (그리고 어디서 볼지 알고 있음) 그러한 아티팩트의 인스턴스를 보여줍니다. 그럼에도 불구하고, 나는이 구현이 이미 수치 적으로 안정적이라는 것을 알았습니다. 나머지 아티팩트는 슬러그 알고리즘을 사용하여 제거 할 수 있으며, 관련 특허로 인해 여기에서 구현되지 않습니다.

이 데모는 또한 밴딩과 같은 성능 최적화를 구현하지 않으며 일부 시나리오와 매우 복잡한 글꼴을 사용할 때 GPU 사용량이 높을 수 있습니다.

지침을 작성하십시오

1. 초크 모듈

프로젝트를 재귀 적으로 복제하여 종속성에 대한 하위 모듈을 초기화합니다 (또는 git submodule update --init 이미 repo를 클로닝 한 경우 Init) :

 git clone --recursive https://github.com/GreenLightning/gpu-font-rendering.git
cd gpu-font-rendering

2. CMAKE를 사용하십시오

 # Note: CMake will create the build directory.
cmake -S . -B build
make -j8 --directory build

Windows에서는 CMake GUI 및/또는 Visual Studio를 대신 사용하고 싶을 수도 있습니다.

Linux에서는 OpenGL 개발을위한 추가 패키지를 설치해야 할 수도 있습니다 (예 : sudo apt-get install xorg-dev libgl1-mesa-dev for ubuntu).

3. 기본 프로젝트 디렉토리에서 실행됩니다

 ./build/main

이 프로그램은 fonts 및 shaders 디렉토리가 리소스를로드하기 위해 현재 디렉토리에 있어야합니다. 검은 창만 받으면 문제가 발생할 가능성이 높습니다. 작업 디렉토리를 확인하고 콘솔에서 오류를 확인하십시오.

Windows 10, Macos Monterey 및 Ubuntu 22.04에서 테스트.