JAXpip install lovely-tensorsou
mamba install lovely-tensorsou
conda install -c conda-forge lovely-tensorsCom que frequência você se encontra depurando o código Pytorch? Você despeja um tensor na saída da célula e vê o seguinte:
numbers tensor([[[-0.3541, -0.3369, -0.4054, ..., -0.5596, -0.4739, 2.2489],
[-0.4054, -0.4226, -0.4911, ..., -0.9192, -0.8507, 2.1633],
[-0.4739, -0.4739, -0.5424, ..., -1.0390, -1.0390, 2.1975],
...,
[-0.9020, -0.8335, -0.9363, ..., -1.4672, -1.2959, 2.2318],
[-0.8507, -0.7822, -0.9363, ..., -1.6042, -1.5014, 2.1804],
[-0.8335, -0.8164, -0.9705, ..., -1.6555, -1.5528, 2.1119]],
[[-0.1975, -0.1975, -0.3025, ..., -0.4776, -0.3725, 2.4111],
[-0.2500, -0.2325, -0.3375, ..., -0.7052, -0.6702, 2.3585],
[-0.3025, -0.2850, -0.3901, ..., -0.7402, -0.8102, 2.3761],
...,
[-0.4251, -0.2325, -0.3725, ..., -1.0903, -1.0203, 2.4286],
[-0.3901, -0.2325, -0.4251, ..., -1.2304, -1.2304, 2.4111],
[-0.4076, -0.2850, -0.4776, ..., -1.2829, -1.2829, 2.3410]],
[[-0.6715, -0.9853, -0.8807, ..., -0.9678, -0.6890, 2.3960],
[-0.7238, -1.0724, -0.9678, ..., -1.2467, -1.0201, 2.3263],
[-0.8284, -1.1247, -1.0201, ..., -1.2641, -1.1596, 2.3786],
...,
[-1.2293, -1.4733, -1.3861, ..., -1.5081, -1.2641, 2.5180],
[-1.1944, -1.4559, -1.4210, ..., -1.6476, -1.4733, 2.4308],
[-1.2293, -1.5256, -1.5081, ..., -1.6824, -1.5256, 2.3611]]])
Foi realmente útil para você, como humano, ver todos esses números?
Qual é a forma? O tamanho?
Quais são as estatísticas?
Algum dos valores é nan ou inf ?
É uma imagem de um homem segurando uma tencha?
import lovely_tensors as lt lt . monkey_patch () numbers # torch.Tensor tensor[3, 196, 196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073
numbers . rgbMelhor, hein?
numbers [ 1 ,: 6 , 1 ] # Still shows values if there are not too many. tensor[6] x∈[-0.443, -0.197] μ=-0.311 σ=0.091 [-0.197, -0.232, -0.285, -0.373, -0.443, -0.338]
spicy = numbers [ 0 ,: 12 , 0 ]. clone ()
spicy [ 0 ] *= 10000
spicy [ 1 ] /= 10000
spicy [ 2 ] = float ( 'inf' )
spicy [ 3 ] = float ( '-inf' )
spicy [ 4 ] = float ( 'nan' )
spicy = spicy . reshape (( 2 , 6 ))
spicy # Spicy stuff tensor[2, 6] n=12 x∈[-3.541e+03, -4.054e-05] μ=-393.842 σ=1.180e+03 +Inf! -Inf! NaN!
torch . zeros ( 10 , 10 ) # A zero tensor - make it obvious tensor[10, 10] n=100 all_zeros
spicy . v # Verbose tensor[2, 6] n=12 x∈[-3.541e+03, -4.054e-05] μ=-393.842 σ=1.180e+03 +Inf! -Inf! NaN!
tensor([[-3.5405e+03, -4.0543e-05, inf, -inf, nan, -6.1093e-01],
[-6.1093e-01, -5.9380e-01, -5.9380e-01, -5.4243e-01, -5.4243e-01, -5.4243e-01]])
spicy . p # The plain old way tensor([[-3.5405e+03, -4.0543e-05, inf, -inf, nan, -6.1093e-01],
[-6.1093e-01, -5.9380e-01, -5.9380e-01, -5.4243e-01, -5.4243e-01, -5.4243e-01]])
named_numbers = numbers . rename ( "C" , "H" , "W" )
named_numbers /home/xl0/mambaforge/envs/lovely-py31-torch25/lib/python3.10/site-packages/torch/_tensor.py:1420: UserWarning: Named tensors and all their associated APIs are an experimental feature and subject to change. Please do not use them for anything important until they are released as stable. (Triggered internally at ../c10/core/TensorImpl.h:1925.)
return super().rename(names)
tensor[C=3, H=196, W=196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073
.deeper numbers . deeper tensor[3, 196, 196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073
tensor[196, 196] n=38416 x∈[-2.118, 2.249] μ=-0.324 σ=1.036
tensor[196, 196] n=38416 x∈[-1.966, 2.429] μ=-0.274 σ=0.973
tensor[196, 196] n=38416 x∈[-1.804, 2.640] μ=-0.567 σ=1.178
# You can go deeper if you need to
# And we can use `.deeper` with named dimensions.
named_numbers . deeper ( 2 ) tensor[C=3, H=196, W=196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073
tensor[H=196, W=196] n=38416 x∈[-2.118, 2.249] μ=-0.324 σ=1.036
tensor[W=196] x∈[-1.912, 2.249] μ=-0.673 σ=0.522
tensor[W=196] x∈[-1.861, 2.163] μ=-0.738 σ=0.418
tensor[W=196] x∈[-1.758, 2.198] μ=-0.806 σ=0.397
tensor[W=196] x∈[-1.656, 2.249] μ=-0.849 σ=0.369
tensor[W=196] x∈[-1.673, 2.198] μ=-0.857 σ=0.357
tensor[W=196] x∈[-1.656, 2.146] μ=-0.848 σ=0.372
tensor[W=196] x∈[-1.433, 2.215] μ=-0.784 σ=0.397
tensor[W=196] x∈[-1.279, 2.249] μ=-0.695 σ=0.486
tensor[W=196] x∈[-1.364, 2.249] μ=-0.637 σ=0.539
...
tensor[H=196, W=196] n=38416 x∈[-1.966, 2.429] μ=-0.274 σ=0.973
tensor[W=196] x∈[-1.861, 2.411] μ=-0.529 σ=0.556
tensor[W=196] x∈[-1.826, 2.359] μ=-0.562 σ=0.473
tensor[W=196] x∈[-1.756, 2.376] μ=-0.622 σ=0.458
tensor[W=196] x∈[-1.633, 2.429] μ=-0.664 σ=0.430
tensor[W=196] x∈[-1.651, 2.376] μ=-0.669 σ=0.399
tensor[W=196] x∈[-1.633, 2.376] μ=-0.701 σ=0.391
tensor[W=196] x∈[-1.563, 2.429] μ=-0.670 σ=0.380
tensor[W=196] x∈[-1.475, 2.429] μ=-0.616 σ=0.386
tensor[W=196] x∈[-1.511, 2.429] μ=-0.593 σ=0.399
...
tensor[H=196, W=196] n=38416 x∈[-1.804, 2.640] μ=-0.567 σ=1.178
tensor[W=196] x∈[-1.717, 2.396] μ=-0.982 σ=0.350
tensor[W=196] x∈[-1.752, 2.326] μ=-1.034 σ=0.314
tensor[W=196] x∈[-1.648, 2.379] μ=-1.086 σ=0.314
tensor[W=196] x∈[-1.630, 2.466] μ=-1.121 σ=0.305
tensor[W=196] x∈[-1.717, 2.448] μ=-1.120 σ=0.302
tensor[W=196] x∈[-1.717, 2.431] μ=-1.166 σ=0.314
tensor[W=196] x∈[-1.560, 2.448] μ=-1.124 σ=0.326
tensor[W=196] x∈[-1.421, 2.431] μ=-1.064 σ=0.383
tensor[W=196] x∈[-1.526, 2.396] μ=-1.047 σ=0.417
...
.rgbA Queston importante - é nosso homem?
numbers . rgb ( numbers ). plt ( numbers + 3 ). plt ( center = "range" ).chans # .chans will map values betwen [-1,1] to colors.
# Make our values fit into that range to avoid clipping.
mean = torch . tensor ( in_stats [ 0 ])[:, None , None ]
std = torch . tensor ( in_stats [ 1 ])[:, None , None ]
numbers_01 = ( numbers * std + mean )
numbers_01 tensor[3, 196, 196] n=115248 (0.4Mb) x∈[0., 1.000] μ=0.361 σ=0.248
numbers_01 . chans # Weights of the second conv layer (64ch -> 128ch) of VGG11,
# grouped per output channel.
weights . chans ( frame_px = 1 , gutter_px = 0 ) lt . chans ( numbers_01 )
numbers . rgb ( in_stats ). fig # matplotlib figure 
( numbers * 0.3 + 0.5 ). chans . fig # matplotlib figure 
numbers . plt . fig . savefig ( 'pretty.svg' ) # Save it !f ile pretty . svg ; rm pretty . svg pretty.svg: SVG Scalable Vector Graphics image
fig = plt . figure ( figsize = ( 8 , 3 ))
fig . set_constrained_layout ( True )
gs = fig . add_gridspec ( 2 , 2 )
ax1 = fig . add_subplot ( gs [ 0 , :])
ax2 = fig . add_subplot ( gs [ 1 , 0 ])
ax3 = fig . add_subplot ( gs [ 1 , 1 :])
ax2 . set_axis_off ()
ax3 . set_axis_off ()
numbers_01 . plt ( ax = ax1 )
numbers_01 . rgb ( ax = ax2 )
numbers_01 . chans ( ax = ax3 );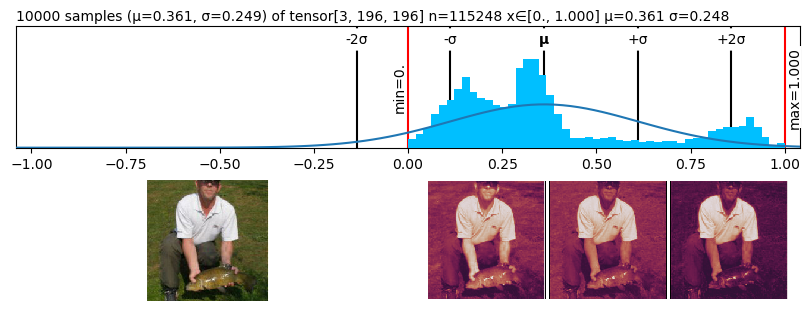
Apenas funciona.
def func ( x ):
return x * 2
if torch . __version__ >= "2.0" :
func = torch . compile ( func )
func ( torch . tensor ([ 1 , 2 , 3 ])) tensor[3] i64 x∈[2, 6] μ=4.000 σ=2.000 [2, 4, 6]
Tensores encantadores instalam um gancho de importação. Definir LOVELY_TENSORS=1 , e ele carregará automaticamente, não é necessário modificar o código:> Nota: Não o defina globalmente, ou todos os scripts do Python que você executará importarão LT e Pytorch, o que diminuirá as coisas.
import torch
x = torch . randn ( 4 , 16 )
print ( x )LOVELY_TENSORS=1 python test.py x: tensor[4, 16] n=64 x∈[-1.652, 1.813] μ=-0.069 σ=0.844
Isso é especialmente útil em combinação com melhores exceções:
import torch
x = torch . randn ( 4 , 16 )
print ( f"x: { x } " )
w = torch . randn ( 15 , 8 )
y = torch . matmul ( x , w ) # Dimension mismatch BETTER_EXCEPTIONS=1 LOVELY_TENSORS=1 python test.py x: tensor[4, 16] n=64 x∈[-1.834, 2.421] μ=0.103 σ=0.896
Traceback (most recent call last):
File "/home/xl0/work/projects/lovely-tensors/test.py", line 7, in <module>
y = torch.matmul(x, w)
│ │ └ tensor[15, 8] n=120 x∈[-2.355, 2.165] μ=0.142 σ=0.989
│ └ tensor[4, 16] n=64 x∈[-1.834, 2.421] μ=0.103 σ=0.896
└ <module 'torch' from '/home/xl0/mambaforge/envs/torch25-py313/lib/python3.12/site-packages/torch/__init__.py'>
RuntimeError: mat1 and mat2 shapes cannot be multiplied (4x16 and 15x8)