Home>Programming related>Python
Download

❤️ Lovely Tensors

Read full docs

More lovely stuff

Working with numbers
  • Numpy: ❤️ Lovely NumPy
  • JAX: ? Lovely JAX
  • TinyGrad: ? Lovely Grad
Community
  • Discord

Install

pip install lovely-tensors

or

mamba install lovely-tensors

or

conda install -c conda-forge lovely-tensors

How to use

How often do you find yourself debugging PyTorch code? You dump a tensor to the cell output, and see this:

numbers
tensor([[[-0.3541, -0.3369, -0.4054,  ..., -0.5596, -0.4739,  2.2489],
         [-0.4054, -0.4226, -0.4911,  ..., -0.9192, -0.8507,  2.1633],
         [-0.4739, -0.4739, -0.5424,  ..., -1.0390, -1.0390,  2.1975],
         ...,
         [-0.9020, -0.8335, -0.9363,  ..., -1.4672, -1.2959,  2.2318],
         [-0.8507, -0.7822, -0.9363,  ..., -1.6042, -1.5014,  2.1804],
         [-0.8335, -0.8164, -0.9705,  ..., -1.6555, -1.5528,  2.1119]],

        [[-0.1975, -0.1975, -0.3025,  ..., -0.4776, -0.3725,  2.4111],
         [-0.2500, -0.2325, -0.3375,  ..., -0.7052, -0.6702,  2.3585],
         [-0.3025, -0.2850, -0.3901,  ..., -0.7402, -0.8102,  2.3761],
         ...,
         [-0.4251, -0.2325, -0.3725,  ..., -1.0903, -1.0203,  2.4286],
         [-0.3901, -0.2325, -0.4251,  ..., -1.2304, -1.2304,  2.4111],
         [-0.4076, -0.2850, -0.4776,  ..., -1.2829, -1.2829,  2.3410]],

        [[-0.6715, -0.9853, -0.8807,  ..., -0.9678, -0.6890,  2.3960],
         [-0.7238, -1.0724, -0.9678,  ..., -1.2467, -1.0201,  2.3263],
         [-0.8284, -1.1247, -1.0201,  ..., -1.2641, -1.1596,  2.3786],
         ...,
         [-1.2293, -1.4733, -1.3861,  ..., -1.5081, -1.2641,  2.5180],
         [-1.1944, -1.4559, -1.4210,  ..., -1.6476, -1.4733,  2.4308],
         [-1.2293, -1.5256, -1.5081,  ..., -1.6824, -1.5256,  2.3611]]])

Was it really useful for you, as a human, to see all these numbers?

What is the shape? The size?
What are the statistics?
Are any of the values nan or inf?
Is it an image of a man holding a tench?

import lovely_tensors as lt
lt.monkey_patch()

Summary

numbers # torch.Tensor
tensor[3, 196, 196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073

numbers.rgb

Better, huh?

numbers[1,:6,1] # Still shows values if there are not too many.
tensor[6] x∈[-0.443, -0.197] μ=-0.311 σ=0.091 [-0.197, -0.232, -0.285, -0.373, -0.443, -0.338]

spicy = numbers[0,:12,0].clone()

spicy[0] *= 10000
spicy[1] /= 10000
spicy[2] = float('inf')
spicy[3] = float('-inf')
spicy[4] = float('nan')

spicy = spicy.reshape((2,6))
spicy # Spicy stuff
tensor[2, 6] n=12 x∈[-3.541e+03, -4.054e-05] μ=-393.842 σ=1.180e+03 +Inf! -Inf! NaN!

torch.zeros(10, 10) # A zero tensor - make it obvious
tensor[10, 10] n=100 all_zeros

spicy.v # Verbose
tensor[2, 6] n=12 x∈[-3.541e+03, -4.054e-05] μ=-393.842 σ=1.180e+03 +Inf! -Inf! NaN!
tensor([[-3.5405e+03, -4.0543e-05,         inf,        -inf,         nan, -6.1093e-01],
        [-6.1093e-01, -5.9380e-01, -5.9380e-01, -5.4243e-01, -5.4243e-01, -5.4243e-01]])

spicy.p # The plain old way
tensor([[-3.5405e+03, -4.0543e-05,         inf,        -inf,         nan, -6.1093e-01],
        [-6.1093e-01, -5.9380e-01, -5.9380e-01, -5.4243e-01, -5.4243e-01, -5.4243e-01]])

Named dimensions

named_numbers = numbers.rename("C", "H","W")
named_numbers
/home/xl0/mambaforge/envs/lovely-py31-torch25/lib/python3.10/site-packages/torch/_tensor.py:1420: UserWarning: Named tensors and all their associated APIs are an experimental feature and subject to change. Please do not use them for anything important until they are released as stable. (Triggered internally at ../c10/core/TensorImpl.h:1925.)
  return super().rename(names)

tensor[C=3, H=196, W=196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073

Going .deeper

numbers.deeper
tensor[3, 196, 196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073
  tensor[196, 196] n=38416 x∈[-2.118, 2.249] μ=-0.324 σ=1.036
  tensor[196, 196] n=38416 x∈[-1.966, 2.429] μ=-0.274 σ=0.973
  tensor[196, 196] n=38416 x∈[-1.804, 2.640] μ=-0.567 σ=1.178

# You can go deeper if you need to
# And we can use `.deeper` with named dimensions.

named_numbers.deeper(2)
tensor[C=3, H=196, W=196] n=115248 (0.4Mb) x∈[-2.118, 2.640] μ=-0.388 σ=1.073
  tensor[H=196, W=196] n=38416 x∈[-2.118, 2.249] μ=-0.324 σ=1.036
    tensor[W=196] x∈[-1.912, 2.249] μ=-0.673 σ=0.522
    tensor[W=196] x∈[-1.861, 2.163] μ=-0.738 σ=0.418
    tensor[W=196] x∈[-1.758, 2.198] μ=-0.806 σ=0.397
    tensor[W=196] x∈[-1.656, 2.249] μ=-0.849 σ=0.369
    tensor[W=196] x∈[-1.673, 2.198] μ=-0.857 σ=0.357
    tensor[W=196] x∈[-1.656, 2.146] μ=-0.848 σ=0.372
    tensor[W=196] x∈[-1.433, 2.215] μ=-0.784 σ=0.397
    tensor[W=196] x∈[-1.279, 2.249] μ=-0.695 σ=0.486
    tensor[W=196] x∈[-1.364, 2.249] μ=-0.637 σ=0.539
    ...
  tensor[H=196, W=196] n=38416 x∈[-1.966, 2.429] μ=-0.274 σ=0.973
    tensor[W=196] x∈[-1.861, 2.411] μ=-0.529 σ=0.556
    tensor[W=196] x∈[-1.826, 2.359] μ=-0.562 σ=0.473
    tensor[W=196] x∈[-1.756, 2.376] μ=-0.622 σ=0.458
    tensor[W=196] x∈[-1.633, 2.429] μ=-0.664 σ=0.430
    tensor[W=196] x∈[-1.651, 2.376] μ=-0.669 σ=0.399
    tensor[W=196] x∈[-1.633, 2.376] μ=-0.701 σ=0.391
    tensor[W=196] x∈[-1.563, 2.429] μ=-0.670 σ=0.380
    tensor[W=196] x∈[-1.475, 2.429] μ=-0.616 σ=0.386
    tensor[W=196] x∈[-1.511, 2.429] μ=-0.593 σ=0.399
    ...
  tensor[H=196, W=196] n=38416 x∈[-1.804, 2.640] μ=-0.567 σ=1.178
    tensor[W=196] x∈[-1.717, 2.396] μ=-0.982 σ=0.350
    tensor[W=196] x∈[-1.752, 2.326] μ=-1.034 σ=0.314
    tensor[W=196] x∈[-1.648, 2.379] μ=-1.086 σ=0.314
    tensor[W=196] x∈[-1.630, 2.466] μ=-1.121 σ=0.305
    tensor[W=196] x∈[-1.717, 2.448] μ=-1.120 σ=0.302
    tensor[W=196] x∈[-1.717, 2.431] μ=-1.166 σ=0.314
    tensor[W=196] x∈[-1.560, 2.448] μ=-1.124 σ=0.326
    tensor[W=196] x∈[-1.421, 2.431] μ=-1.064 σ=0.383
    tensor[W=196] x∈[-1.526, 2.396] μ=-1.047 σ=0.417
    ...

Now in .rgb color

The important queston - is it our man?

numbers.rgb
(numbers).plt
(numbers+3).plt(center="range")

See the .chans

# .chans will map values betwen [-1,1] to colors.
# Make our values fit into that range to avoid clipping.
mean = torch.tensor(in_stats[0])[:,None,None]
std = torch.tensor(in_stats[1])[:,None,None]
numbers_01 = (numbers*std + mean)
numbers_01
tensor[3, 196, 196] n=115248 (0.4Mb) x∈[0., 1.000] μ=0.361 σ=0.248

numbers_01.chans
# Weights of the second conv layer (64ch -> 128ch) of VGG11,
# grouped per output channel.
weights.chans(frame_px=1, gutter_px=0)
lt.chans(numbers_01)

Matplotlib integration | Docs

numbers.rgb(in_stats).fig # matplotlib figure

(numbers*0.3+0.5).chans.fig # matplotlib figure

numbers.plt.fig.savefig('pretty.svg') # Save it
!file pretty.svg; rm pretty.svg
pretty.svg: SVG Scalable Vector Graphics image

Add content to existing Axes

fig = plt.figure(figsize=(8,3))
fig.set_constrained_layout(True)
gs = fig.add_gridspec(2,2)
ax1 = fig.add_subplot(gs[0, :])
ax2 = fig.add_subplot(gs[1, 0])
ax3 = fig.add_subplot(gs[1,1:])

ax2.set_axis_off()
ax3.set_axis_off()

numbers_01.plt(ax=ax1)
numbers_01.rgb(ax=ax2)
numbers_01.chans(ax=ax3);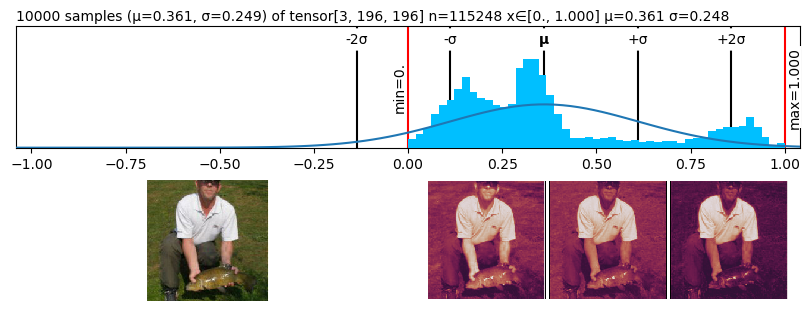

torch.compile()

Just works.

def func(x):
    return x*2

if torch.__version__ >= "2.0":
    func = torch.compile(func)

func(torch.tensor([1,2,3]))
tensor[3] i64 x∈[2, 6] μ=4.000 σ=2.000 [2, 4, 6]

Inport hook

Lovely tensors installes an import hook. Set LOVELY_TENSORS=1, and it will load automatically, no need to modify the code: > Note: Don’t set it globally, or all python scripts you run will import LT and PyTorch, which will slow things down.

import torch

x = torch.randn(4, 16)
print(x)
LOVELY_TENSORS=1 python test.py
x: tensor[4, 16] n=64 x∈[-1.652, 1.813] μ=-0.069 σ=0.844

This is especially useful in combination with Better Exceptions:

import torch

x = torch.randn(4, 16)
print(f"x: {x}")

w = torch.randn(15, 8) 
y = torch.matmul(x, w) # Dimension mismatch
BETTER_EXCEPTIONS=1  LOVELY_TENSORS=1 python test.py 
x: tensor[4, 16] n=64 x∈[-1.834, 2.421] μ=0.103 σ=0.896
Traceback (most recent call last):
  File "/home/xl0/work/projects/lovely-tensors/test.py", line 7, in <module>
    y = torch.matmul(x, w)
        │            │  └ tensor[15, 8] n=120 x∈[-2.355, 2.165] μ=0.142 σ=0.989
        │            └ tensor[4, 16] n=64 x∈[-1.834, 2.421] μ=0.103 σ=0.896
        └ <module 'torch' from '/home/xl0/mambaforge/envs/torch25-py313/lib/python3.12/site-packages/torch/__init__.py'>
RuntimeError: mat1 and mat2 shapes cannot be multiplied (4x16 and 15x8)
Expand
Additional Information
Related Applications
Recommended for You
Related Information All