skpr -Download - skpr Source Code Download

skpr

PowerBuilder

v1.7.0

Herunterladen

SKPR

Überblick

SKPR ist ein Open -Source -Design der Experimenten -Suite zur Erzeugung und Bewertung optimaler Designs in R. Hier ist eine Stichprobe dessen, was SKPR anbietet:

Generiert und bewertet D, I, A, Alias, E, T und G Optimale Designs sowie benutzerdefinierte benutzerdefinierte Optimalitätskriterien.
Unterstützt die Erzeugung und Bewertung von Split/Split-Split/…/N-Split-Plot-Designs.
Enthält parametrische und monte -Carlo -Leistungsbewertungsfunktionen und unterstützt die Berechnung der Leistung für zensierte Antworten.
Bietet dem Benutzer einen erweiterbaren Framework, mit dem Monte Carlo Power mit seinen eigenen Bibliotheken bewertet werden kann.
Enthält eine glänzende grafische Benutzeroberfläche, SKPRGUI, die den R-Code automatisch generiert, um das Design zu erstellen und zu bewerten, um die Benutzerfreundlichkeit zu verbessern und die Reproduzierbarkeit zu verbessern.

Installation

 # To install:
install.packages( " skpr " )

# To install the latest version from Github:
# install.packages("devtools")
devtools :: install_github( " tylermorganwall/skpr " )

Funktionen

gen_design() generiert optimale Designs aus einem Kandidatensatz, bei dem ein Modell und die gewünschte Anzahl von Läufen.
eval_design() bewertet die Stromversorgung parametrisch für lineare Modelle für normale und splitische Entwürfe.
eval_design_mc() bewertet die Leistung mit einer Monte -Carlo -Simulation für lineare und verallgemeinerte lineare Modelle. Diese Funktion unterstützt auch die Berechnung der Leistung für Split-Plot-Designs unter Verwendung von REML.
eval_design_survival_mc() bewertet die Leistung mit einer Monte -Carlo -Simulation, sodass der Benutzer einen Punkt angeben kann, an dem die Daten zensiert werden.
eval_design_custom_mc() ermöglicht es dem Benutzer, seine eigenen Bibliotheken zu importieren und das von SKPR bereitgestellte Monte -Carlo -Framework zur Berechnung der Stromversorgung zu verwenden.
calculate_power_curves() bietet eine Schnittstelle zur Automatisierung der Erzeugung und Bewertung von Designs zur Erstellung von Strom- und Stichprobengröße und Effektgrößenkurven.
skprGUI() öffnet die GUI entweder in Rstudio oder in einem externen Browser.

Wenn zusätzlich ist, bietet das Paket zwei Funktionen, um gemeinsame Handlungen im Zusammenhang mit Designs zu generieren:

plot_correlations() erzeugt eine Farbkarte mit Korrelationen zwischen Variablen.
plot_fds() erzeugt den Bruchteil des Entwurfsraumdiagramms für ein bestimmtes Design.

## SKPRGUI

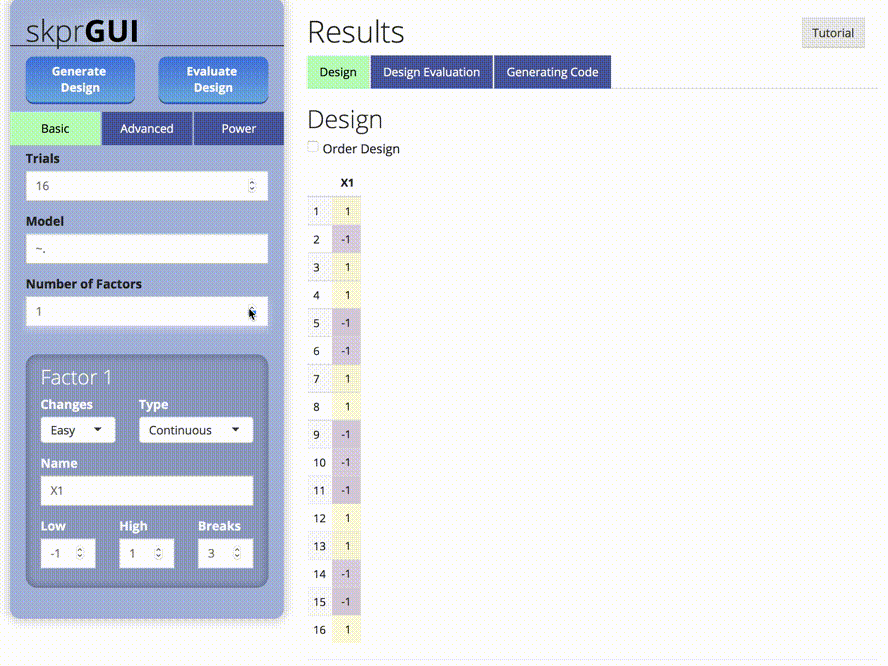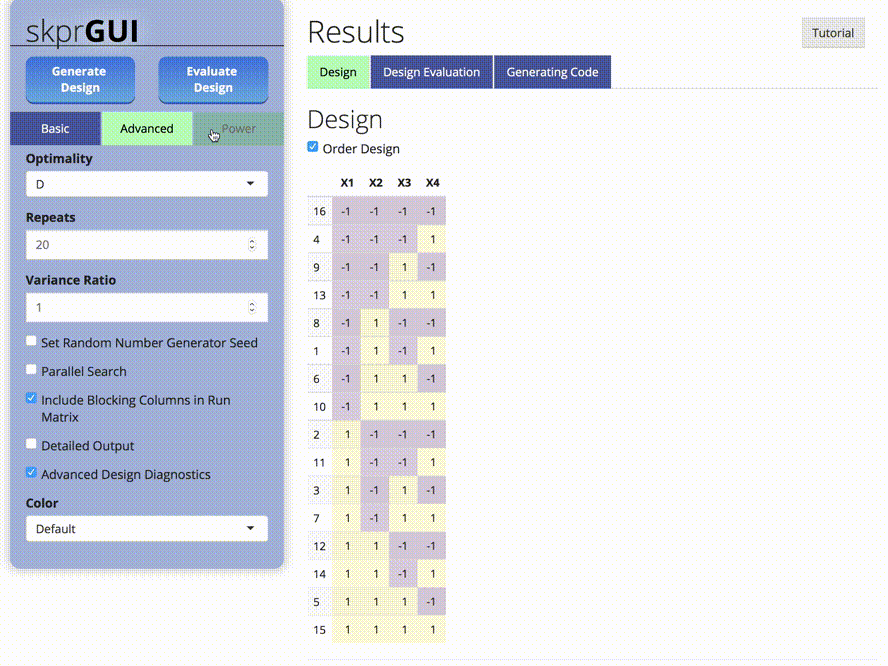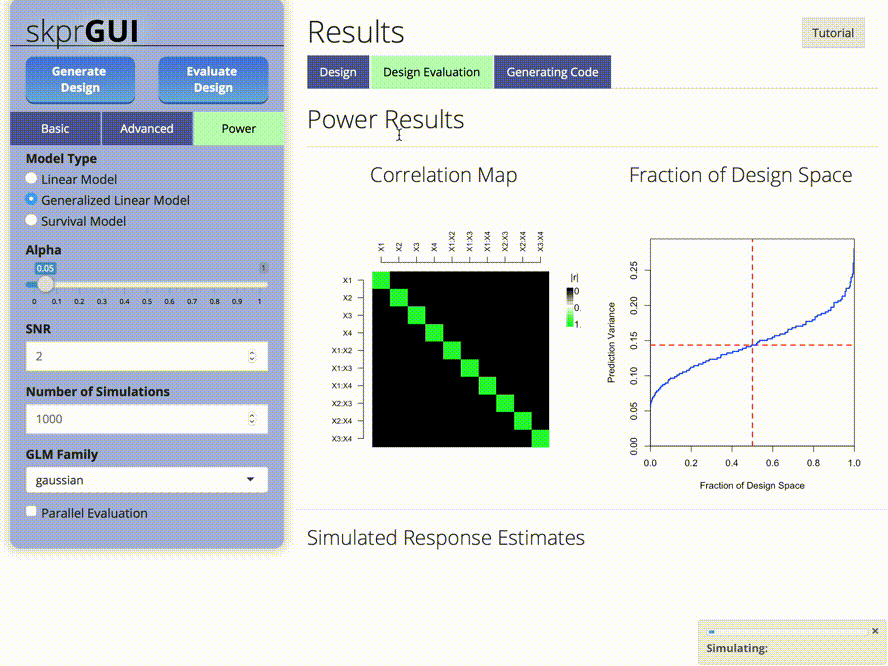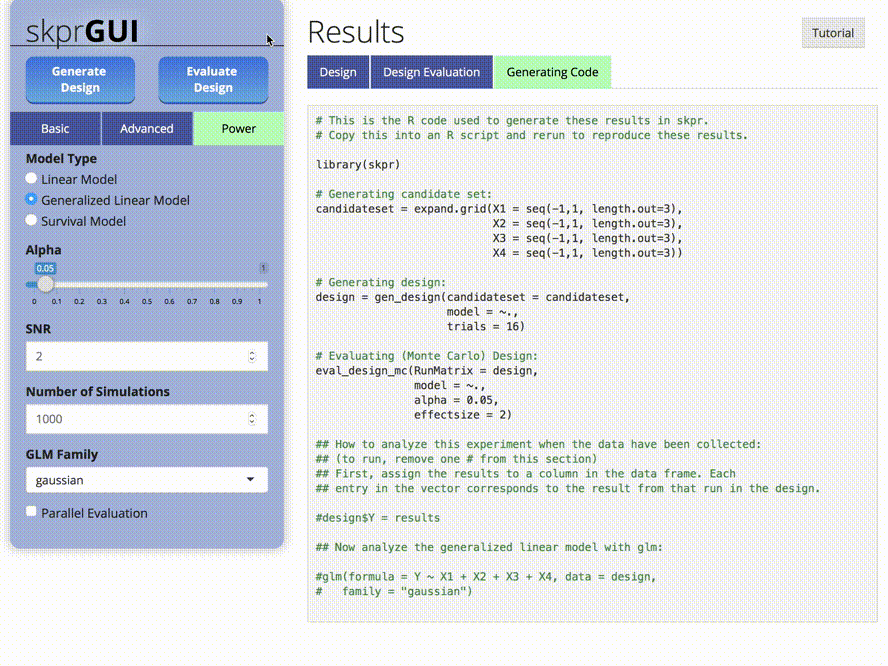
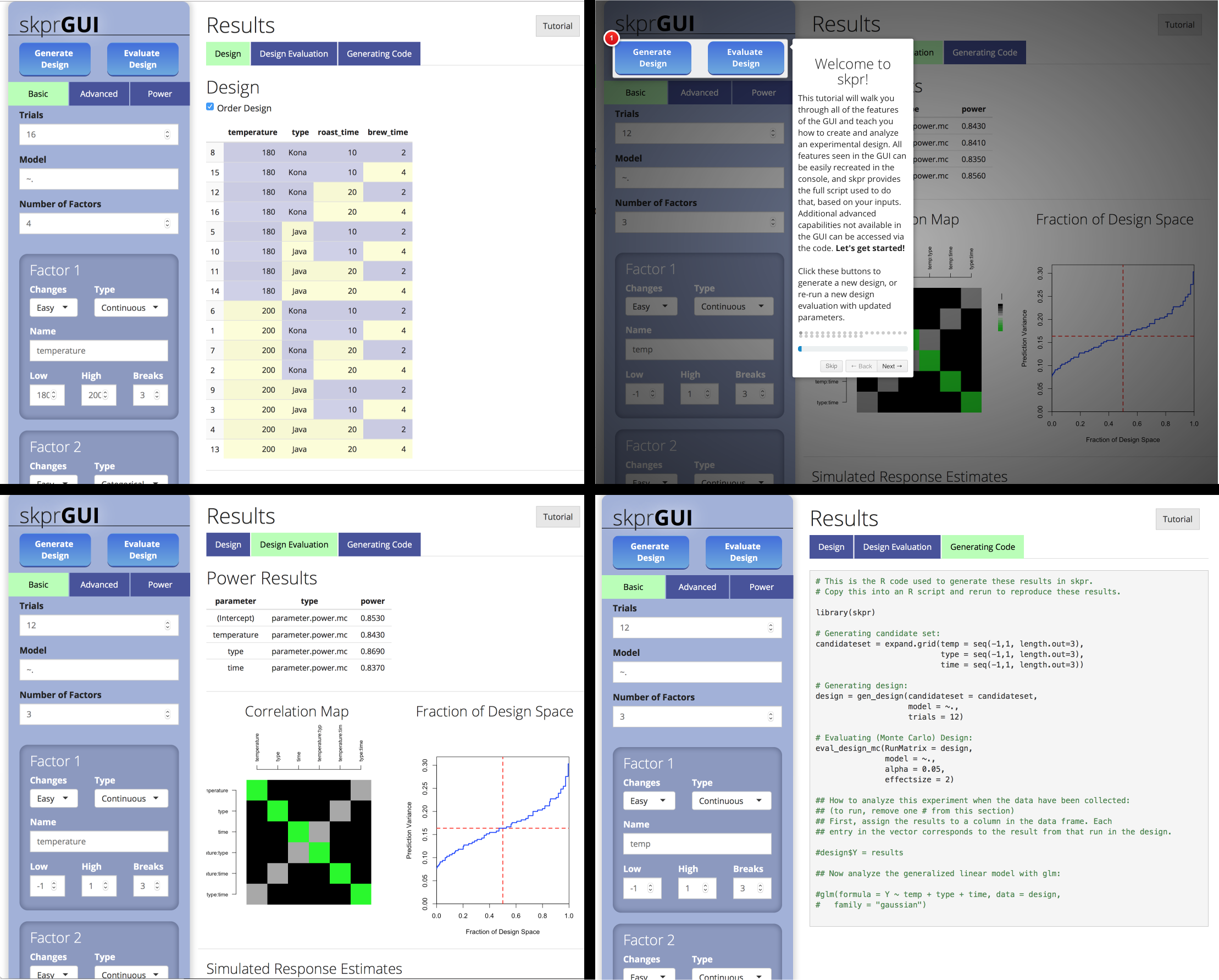
skprGUI() bietet eine grafische Benutzeroberfläche, um auf alle Hauptfunktionen von SKPR zugreifen zu können. Ein interaktives Tutorial wird bereitgestellt, um den Benutzer mit der verfügbaren Funktionalität vertraut zu machen. Geben Sie skprGUI() ein, um zu beginnen. Screenshots:

Verwendung

library( skpr )

# Generate a candidate set of all potential design points to be considered in the experiment
# The hypothetical experiment is determining what affects the caffeine content in coffee
candidate_set = expand.grid( temp = c( 80 , 90 , 100 ), 
                            type = c( " Kona " , " Java " ),
                            beansize = c( " Large " , " Medium " , " Small " ))
candidate_set
# >    temp type beansize
# > 1    80 Kona    Large
# > 2    90 Kona    Large
# > 3   100 Kona    Large
# > 4    80 Java    Large
# > 5    90 Java    Large
# > 6   100 Java    Large
# > 7    80 Kona   Medium
# > 8    90 Kona   Medium
# > 9   100 Kona   Medium
# > 10   80 Java   Medium
# > 11   90 Java   Medium
# > 12  100 Java   Medium
# > 13   80 Kona    Small
# > 14   90 Kona    Small
# > 15  100 Kona    Small
# > 16   80 Java    Small
# > 17   90 Java    Small
# > 18  100 Java    Small

# Generate the design (default D-optimal)
design = gen_design( candidateset = candidate_set , 
                    model = ~ temp + type + beansize ,
                    trials = 12 )
design
# >    temp type beansize
# > 1    80 Java   Medium
# > 2   100 Java    Large
# > 3   100 Java    Small
# > 4    80 Java    Large
# > 5    80 Kona   Medium
# > 6    80 Kona    Small
# > 7   100 Kona    Small
# > 8   100 Kona   Medium
# > 9    80 Kona    Large
# > 10  100 Java   Medium
# > 11  100 Kona    Large
# > 12   80 Java    Small

# Evaluate power for the design with an allowable type-I error of 5% (default)
eval_design( design )
# >     parameter            type     power
# > 1 (Intercept)    effect.power 0.8424665
# > 2        temp    effect.power 0.8424665
# > 3        type    effect.power 0.8424665
# > 4    beansize    effect.power 0.5165386
# > 5 (Intercept) parameter.power 0.8424665
# > 6        temp parameter.power 0.8424665
# > 7       type1 parameter.power 0.8424665
# > 8   beansize1 parameter.power 0.5593966
# > 9   beansize2 parameter.power 0.5593966
# > ============Evaluation Info============
# > * Alpha = 0.05 * Trials = 12 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize 
# > * Anticipated Coefficients = c(1, 1, 1, 1, -1) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `lm(...)` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")`

# Evaluate power for the design using a Monte Carlo simulation. 
# Here, we set the effect size (here, the signal-to-noise ratio) to 1.5.
eval_design_mc( design , effectsize = 1.5 )
# >     parameter               type power
# > 1 (Intercept)    effect.power.mc 0.600
# > 2        temp    effect.power.mc 0.612
# > 3        type    effect.power.mc 0.610
# > 4    beansize    effect.power.mc 0.316
# > 5 (Intercept) parameter.power.mc 0.600
# > 6        temp parameter.power.mc 0.612
# > 7       type1 parameter.power.mc 0.610
# > 8   beansize1 parameter.power.mc 0.359
# > 9   beansize2 parameter.power.mc 0.354
# > ===========Evaluation Info============
# > * Alpha = 0.05 * Trials = 12 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize 
# > * Anticipated Coefficients = c(0.750, 0.750, 0.750, 0.750, -0.750) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `lm(...)` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")`

# Evaluate power for the design using a Monte Carlo simulation, for a non-normal response. 
# Here, we also increase the number of simululations to improve the precision of the results.
eval_design_mc( design , nsim = 5000 , glmfamily = " poisson " , effectsize = c( 2 , 6 ))
# >     parameter               type  power
# > 1 (Intercept)    effect.power.mc 0.9968
# > 2        temp    effect.power.mc 0.9826
# > 3        type    effect.power.mc 0.9832
# > 4    beansize    effect.power.mc 0.8502
# > 5 (Intercept) parameter.power.mc 0.9968
# > 6        temp parameter.power.mc 0.9826
# > 7       type1 parameter.power.mc 0.9832
# > 8   beansize1 parameter.power.mc 0.8842
# > 9   beansize2 parameter.power.mc 0.7052
# > ============Evaluation Info============
# > * Alpha = 0.05 * Trials = 12 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize 
# > * Anticipated Coefficients = c(1.242, 0.549, 0.549, 0.549, -0.549) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `glm(..., family = "poisson")` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")`

# skpr was designed to operate with the pipe (|>) in mind. 
# Here is an example of an entire design of experiments analysis in three lines:

expand.grid( temp = c( 80 , 90 , 100 ), type = c( " Kona " , " Java " ), beansize = c( " Large " , " Medium " , " Small " )) | >
  gen_design( model = ~ temp + type + beansize + beansize : type + I( temp ^ 2 ), trials = 24 , optimality = " I " ) | >
  eval_design_mc( detailedoutput = TRUE )
# >          parameter               type power anticoef alpha glmfamily trials
# > 1      (Intercept)    effect.power.mc 0.912       NA  0.05  gaussian     24
# > 2             temp    effect.power.mc 0.927       NA  0.05  gaussian     24
# > 3             type    effect.power.mc 0.997       NA  0.05  gaussian     24
# > 4         beansize    effect.power.mc 0.935       NA  0.05  gaussian     24
# > 5        I(temp^2)    effect.power.mc 0.637       NA  0.05  gaussian     24
# > 6    type:beansize    effect.power.mc 0.913       NA  0.05  gaussian     24
# > 7      (Intercept) parameter.power.mc 0.912        1  0.05  gaussian     24
# > 8             temp parameter.power.mc 0.927        1  0.05  gaussian     24
# > 9            type1 parameter.power.mc 0.997        1  0.05  gaussian     24
# > 10       beansize1 parameter.power.mc 0.917        1  0.05  gaussian     24
# > 11       beansize2 parameter.power.mc 0.913       -1  0.05  gaussian     24
# > 12       I(temp^2) parameter.power.mc 0.637        1  0.05  gaussian     24
# > 13 type1:beansize1 parameter.power.mc 0.899        1  0.05  gaussian     24
# > 14 type1:beansize2 parameter.power.mc 0.902       -1  0.05  gaussian     24
# >    nsim blocking error_adjusted_alpha power_lcb power_ucb
# > 1  1000    FALSE                 0.05 0.8927052 0.9288249
# > 2  1000    FALSE                 0.05 0.9090858 0.9423464
# > 3  1000    FALSE                 0.05 0.9912580 0.9993809
# > 4  1000    FALSE                 0.05 0.9178989 0.9494797
# > 5  1000    FALSE                 0.05 0.6063275 0.6668632
# > 6  1000    FALSE                 0.05 0.8937921 0.9297315
# > 7  1000    FALSE                 0.05 0.8927052 0.9288249
# > 8  1000    FALSE                 0.05 0.9090858 0.9423464
# > 9  1000    FALSE                 0.05 0.9912580 0.9993809
# > 10 1000    FALSE                 0.05 0.8981467 0.9333511
# > 11 1000    FALSE                 0.05 0.8937921 0.9297315
# > 12 1000    FALSE                 0.05 0.6063275 0.6668632
# > 13 1000    FALSE                 0.05 0.8786332 0.9169799
# > 14 1000    FALSE                 0.05 0.8818715 0.9197225
# > =========================================================Evaluation Info==========================================================
# > * Alpha = 0.05 * Trials = 24 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize + type:beansize + I(temp^2) 
# > * Anticipated Coefficients = c(1, 1, 1, 1, -1, 1, 1, -1) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `lm(...)` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")` 
# > * MC Power CI Confidence = 95%