Beranda>Terkait pemrograman>Pembangun Kekuatan
Unduh

skpr

Ringkasan

SKPR adalah desain open source dari eksperimen suite untuk menghasilkan dan mengevaluasi desain optimal di R. Berikut ini adalah contoh dari apa yang ditawarkan SKPR:

  • Menghasilkan dan mengevaluasi desain d, i, a, alias, e, t, dan g, serta kriteria optimalitas khusus yang ditentukan pengguna.
  • Mendukung pembuatan dan evaluasi desain plot split/split-split/…/n-split.
  • Termasuk fungsi evaluasi daya parametrik dan Monte Carlo, dan mendukung daya penghitungan untuk tanggapan yang disensor.
  • Menyediakan kerangka kerja yang dapat diperluas bagi pengguna untuk mengevaluasi kekuatan Monte Carlo menggunakan perpustakaan mereka sendiri.
  • Termasuk antarmuka pengguna grafis yang mengkilap, SKPRGUI, yang secara otomatis menghasilkan kode R yang digunakan untuk membuat dan mengevaluasi desain untuk meningkatkan kemudahan penggunaan dan meningkatkan reproduktifitas.

Instalasi 

 # To install:
install.packages( " skpr " )

# To install the latest version from Github:
# install.packages("devtools")
devtools :: install_github( " tylermorganwall/skpr " )

Fungsi

  • gen_design() menghasilkan desain optimal dari kandidat set, diberi model dan jumlah berjalan yang diinginkan.
  • eval_design() mengevaluasi daya secara parametrik untuk model linier, untuk desain normal dan split-plot.
  • eval_design_mc() mengevaluasi daya dengan simulasi Monte Carlo, untuk model linier linier dan umum. Fungsi ini juga mendukung daya penghitungan untuk desain split-plot menggunakan REML.
  • eval_design_survival_mc() mengevaluasi daya dengan simulasi Monte Carlo, yang memungkinkan pengguna untuk menentukan titik di mana data disensor.
  • eval_design_custom_mc() memungkinkan pengguna untuk mengimpor perpustakaan mereka sendiri dan menggunakan kerangka kerja Monte Carlo yang disediakan oleh SKPR untuk menghitung daya.
  • calculate_power_curves() menyediakan antarmuka untuk mengotomatisasi generasi dan evaluasi desain untuk membuat daya versus ukuran sampel dan kurva ukuran efek.
  • skprGUI() membuka GUI baik di rstudio atau browser eksternal.

Jika penambahan, paket ini menawarkan dua fungsi untuk menghasilkan plot umum yang terkait dengan desain:

  • plot_correlations() menghasilkan peta warna korelasi antar variabel.
  • plot_fds() menghasilkan fraksi plot ruang desain untuk desain yang diberikan.

## skprgui

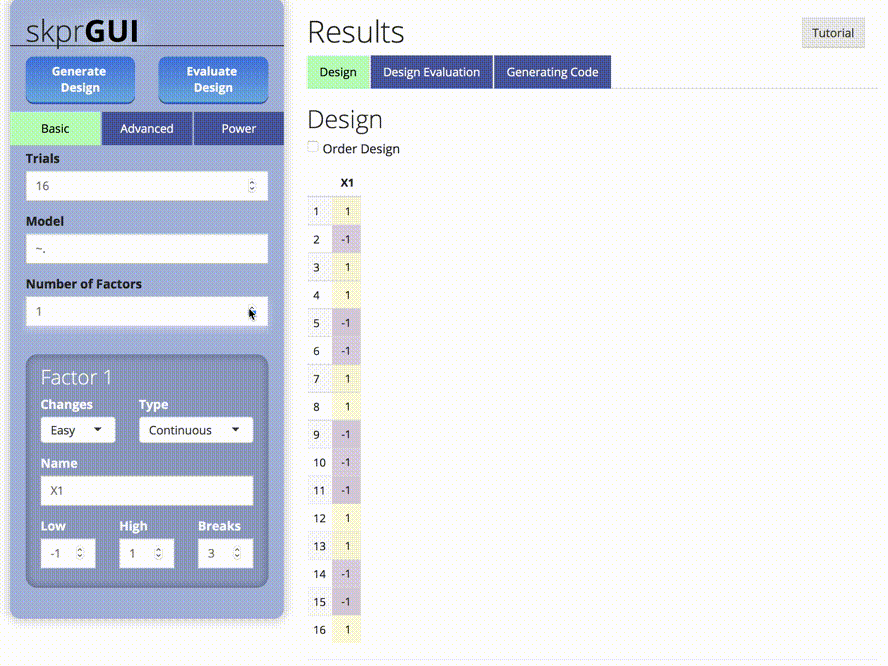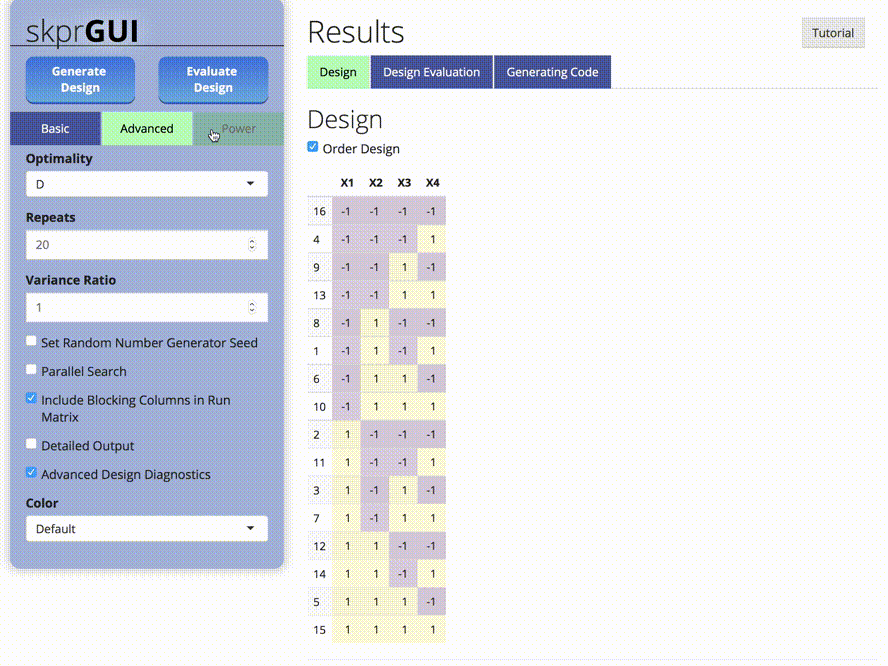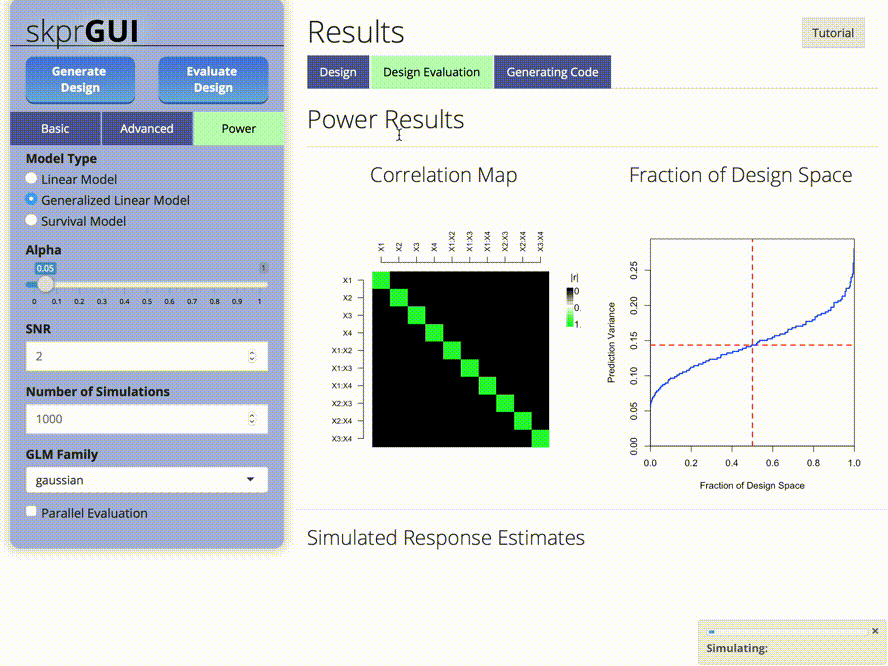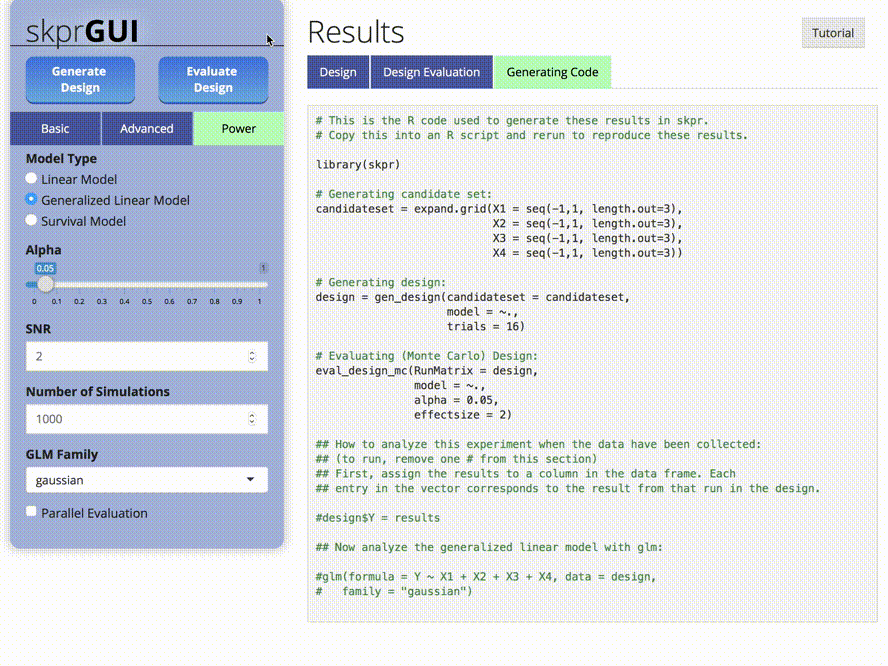
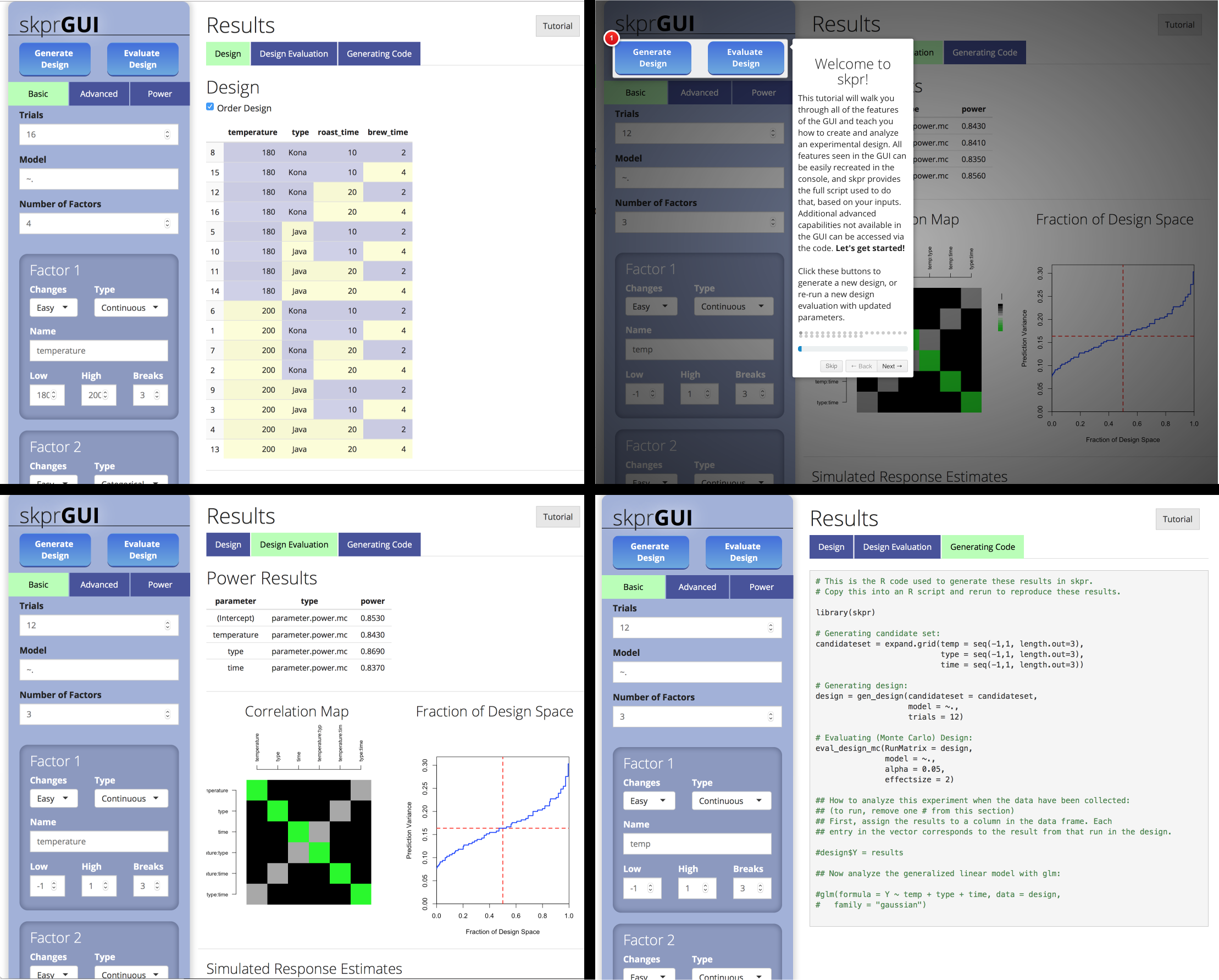
skprGUI() menyediakan antarmuka pengguna grafis untuk mengakses semua fitur utama SKPR. Tutorial interaktif disediakan untuk membiasakan pengguna dengan fungsionalitas yang tersedia. Ketik skprGUI() untuk memulai. Tangkapan layar:

Penggunaan 

library( skpr )

# Generate a candidate set of all potential design points to be considered in the experiment
# The hypothetical experiment is determining what affects the caffeine content in coffee
candidate_set = expand.grid( temp = c( 80 , 90 , 100 ), 
                            type = c( " Kona " , " Java " ),
                            beansize = c( " Large " , " Medium " , " Small " ))
candidate_set
# >    temp type beansize
# > 1    80 Kona    Large
# > 2    90 Kona    Large
# > 3   100 Kona    Large
# > 4    80 Java    Large
# > 5    90 Java    Large
# > 6   100 Java    Large
# > 7    80 Kona   Medium
# > 8    90 Kona   Medium
# > 9   100 Kona   Medium
# > 10   80 Java   Medium
# > 11   90 Java   Medium
# > 12  100 Java   Medium
# > 13   80 Kona    Small
# > 14   90 Kona    Small
# > 15  100 Kona    Small
# > 16   80 Java    Small
# > 17   90 Java    Small
# > 18  100 Java    Small

# Generate the design (default D-optimal)
design = gen_design( candidateset = candidate_set , 
                    model = ~ temp + type + beansize ,
                    trials = 12 )
design
# >    temp type beansize
# > 1    80 Java   Medium
# > 2   100 Java    Large
# > 3   100 Java    Small
# > 4    80 Java    Large
# > 5    80 Kona   Medium
# > 6    80 Kona    Small
# > 7   100 Kona    Small
# > 8   100 Kona   Medium
# > 9    80 Kona    Large
# > 10  100 Java   Medium
# > 11  100 Kona    Large
# > 12   80 Java    Small

# Evaluate power for the design with an allowable type-I error of 5% (default)
eval_design( design )
# >     parameter            type     power
# > 1 (Intercept)    effect.power 0.8424665
# > 2        temp    effect.power 0.8424665
# > 3        type    effect.power 0.8424665
# > 4    beansize    effect.power 0.5165386
# > 5 (Intercept) parameter.power 0.8424665
# > 6        temp parameter.power 0.8424665
# > 7       type1 parameter.power 0.8424665
# > 8   beansize1 parameter.power 0.5593966
# > 9   beansize2 parameter.power 0.5593966
# > ============Evaluation Info============
# > * Alpha = 0.05 * Trials = 12 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize 
# > * Anticipated Coefficients = c(1, 1, 1, 1, -1) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `lm(...)` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")`

# Evaluate power for the design using a Monte Carlo simulation. 
# Here, we set the effect size (here, the signal-to-noise ratio) to 1.5.
eval_design_mc( design , effectsize = 1.5 )
# >     parameter               type power
# > 1 (Intercept)    effect.power.mc 0.600
# > 2        temp    effect.power.mc 0.612
# > 3        type    effect.power.mc 0.610
# > 4    beansize    effect.power.mc 0.316
# > 5 (Intercept) parameter.power.mc 0.600
# > 6        temp parameter.power.mc 0.612
# > 7       type1 parameter.power.mc 0.610
# > 8   beansize1 parameter.power.mc 0.359
# > 9   beansize2 parameter.power.mc 0.354
# > ===========Evaluation Info============
# > * Alpha = 0.05 * Trials = 12 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize 
# > * Anticipated Coefficients = c(0.750, 0.750, 0.750, 0.750, -0.750) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `lm(...)` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")`

# Evaluate power for the design using a Monte Carlo simulation, for a non-normal response. 
# Here, we also increase the number of simululations to improve the precision of the results.
eval_design_mc( design , nsim = 5000 , glmfamily = " poisson " , effectsize = c( 2 , 6 ))
# >     parameter               type  power
# > 1 (Intercept)    effect.power.mc 0.9968
# > 2        temp    effect.power.mc 0.9826
# > 3        type    effect.power.mc 0.9832
# > 4    beansize    effect.power.mc 0.8502
# > 5 (Intercept) parameter.power.mc 0.9968
# > 6        temp parameter.power.mc 0.9826
# > 7       type1 parameter.power.mc 0.9832
# > 8   beansize1 parameter.power.mc 0.8842
# > 9   beansize2 parameter.power.mc 0.7052
# > ============Evaluation Info============
# > * Alpha = 0.05 * Trials = 12 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize 
# > * Anticipated Coefficients = c(1.242, 0.549, 0.549, 0.549, -0.549) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `glm(..., family = "poisson")` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")`

# skpr was designed to operate with the pipe (|>) in mind. 
# Here is an example of an entire design of experiments analysis in three lines:

expand.grid( temp = c( 80 , 90 , 100 ), type = c( " Kona " , " Java " ), beansize = c( " Large " , " Medium " , " Small " )) | >
  gen_design( model = ~ temp + type + beansize + beansize : type + I( temp ^ 2 ), trials = 24 , optimality = " I " ) | >
  eval_design_mc( detailedoutput = TRUE )
# >          parameter               type power anticoef alpha glmfamily trials
# > 1      (Intercept)    effect.power.mc 0.912       NA  0.05  gaussian     24
# > 2             temp    effect.power.mc 0.927       NA  0.05  gaussian     24
# > 3             type    effect.power.mc 0.997       NA  0.05  gaussian     24
# > 4         beansize    effect.power.mc 0.935       NA  0.05  gaussian     24
# > 5        I(temp^2)    effect.power.mc 0.637       NA  0.05  gaussian     24
# > 6    type:beansize    effect.power.mc 0.913       NA  0.05  gaussian     24
# > 7      (Intercept) parameter.power.mc 0.912        1  0.05  gaussian     24
# > 8             temp parameter.power.mc 0.927        1  0.05  gaussian     24
# > 9            type1 parameter.power.mc 0.997        1  0.05  gaussian     24
# > 10       beansize1 parameter.power.mc 0.917        1  0.05  gaussian     24
# > 11       beansize2 parameter.power.mc 0.913       -1  0.05  gaussian     24
# > 12       I(temp^2) parameter.power.mc 0.637        1  0.05  gaussian     24
# > 13 type1:beansize1 parameter.power.mc 0.899        1  0.05  gaussian     24
# > 14 type1:beansize2 parameter.power.mc 0.902       -1  0.05  gaussian     24
# >    nsim blocking error_adjusted_alpha power_lcb power_ucb
# > 1  1000    FALSE                 0.05 0.8927052 0.9288249
# > 2  1000    FALSE                 0.05 0.9090858 0.9423464
# > 3  1000    FALSE                 0.05 0.9912580 0.9993809
# > 4  1000    FALSE                 0.05 0.9178989 0.9494797
# > 5  1000    FALSE                 0.05 0.6063275 0.6668632
# > 6  1000    FALSE                 0.05 0.8937921 0.9297315
# > 7  1000    FALSE                 0.05 0.8927052 0.9288249
# > 8  1000    FALSE                 0.05 0.9090858 0.9423464
# > 9  1000    FALSE                 0.05 0.9912580 0.9993809
# > 10 1000    FALSE                 0.05 0.8981467 0.9333511
# > 11 1000    FALSE                 0.05 0.8937921 0.9297315
# > 12 1000    FALSE                 0.05 0.6063275 0.6668632
# > 13 1000    FALSE                 0.05 0.8786332 0.9169799
# > 14 1000    FALSE                 0.05 0.8818715 0.9197225
# > =========================================================Evaluation Info==========================================================
# > * Alpha = 0.05 * Trials = 24 * Blocked = FALSE 
# > * Evaluating Model = ~temp + type + beansize + type:beansize + I(temp^2) 
# > * Anticipated Coefficients = c(1, 1, 1, 1, -1, 1, 1, -1) 
# > * Contrasts = `contr.sum` 
# > * Parameter Analysis Method = `lm(...)` 
# > * Effect Analysis Method = `car::Anova(fit, type = "III")` 
# > * MC Power CI Confidence = 95%

Memperluas
Informasi Tambahan
Aplikasi Terkait
Direkomendasikan untuk Anda
Informasi Terkait Semua