siamese triplet
1.0.0
Pytorch Implémentation de réseaux siamois et triplet pour l'apprentissage des intérêts.
Les réseaux siamois et triplet sont utiles pour apprendre les mappages de l'image à un espace euclidien compact où les distances correspondent à une mesure de la similitude [2]. Les intégres formés de cette manière peuvent être utilisés comme vecteurs de caractéristiques pour les tâches d'apprentissage de classification ou à quelques coups.
Nécessite Pytorch 0.4 avec TorchVision 0.2.1
Pour Pytorch 0.3 Compatibilité Céche à coche Torch-0.3.1
Nous allons entraîner des intégres sur un ensemble de données MNIST. Des expériences ont été exécutées dans Jupyter Notebook.
Nous allons passer par l'apprentissage des intérêts supervisés des fonctionnalités en utilisant différentes fonctions de perte sur l'ensemble de données MNIST. Ceci est juste à des fins de visualisation, nous utiliserons donc des intégres bidimensionnels qui n'est pas le meilleur choix en pratique.
Pour chaque expérience, le même réseau d'incorporation est utilisé (32 Conv 5x5 -> Prelu -> Maxpool 2x2 -> 64 Conv 5x5 -> Prelu -> Maxpool 2x2 -> dense 256 -> Prelu -> dense 256 -> Prelu -> Dense 2) et nous ne effectuons aucune recherche hyperparamètre.
Nous ajoutons une couche entièrement connectée avec le nombre de classes et formons le réseau pour la classification avec SoftMax et Cross-Entropy. Le réseau s'entraîne à une précision de ~ 99%. Nous extraissons des incorporations en 2 dimensions de l'avant-dernière couche:
Ensemble de train:
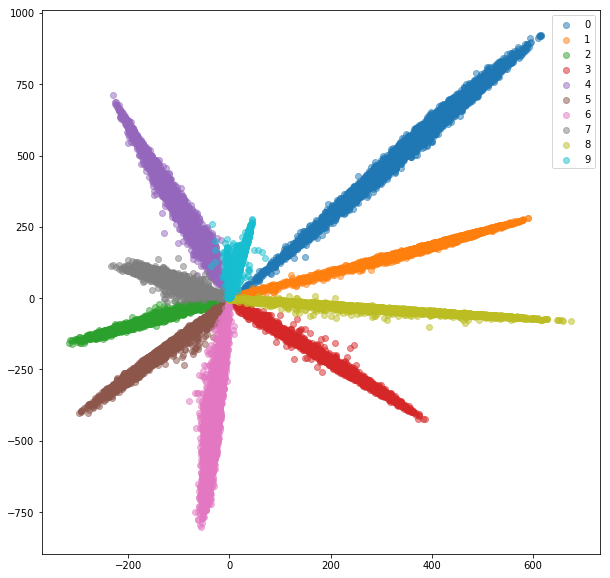
Ensemble de tests:
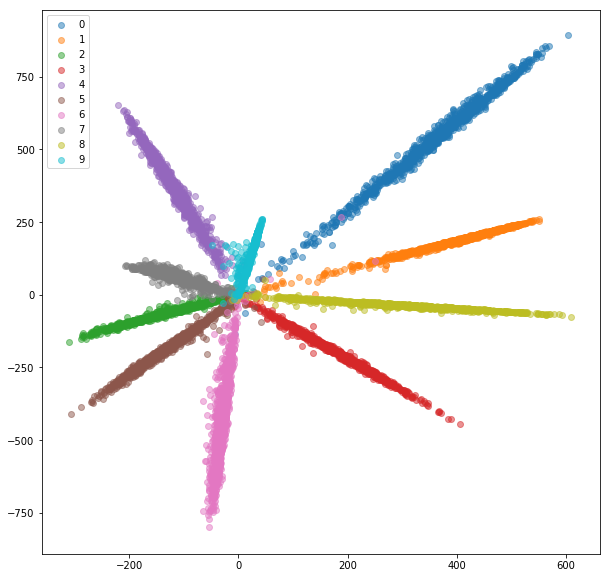
Bien que les intérêts semblent séparables (ce pour quoi nous les avons formés), ils n'ont pas de bonnes propriétés métriques. Ils pourraient ne pas être le meilleur choix en tant que descripteur pour les nouvelles classes.
Maintenant, nous allons entraîner un réseau siamois qui prend une paire d'images et entraîne les intérêts afin que la distance entre eux soit minimisée si elles sont de la même classe et sont supérieures à une valeur de marge si elles représentent des classes différentes. Nous allons minimiser une fonction de perte contrastive [1]:
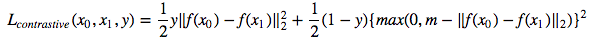
La classe Siamesemiste échantillonne des paires positives et négatives aléatoires qui sont ensuite transmises au réseau siamois.
Après 20 époques de formation, voici les intérêts que nous obtenons pour un ensemble de formation:
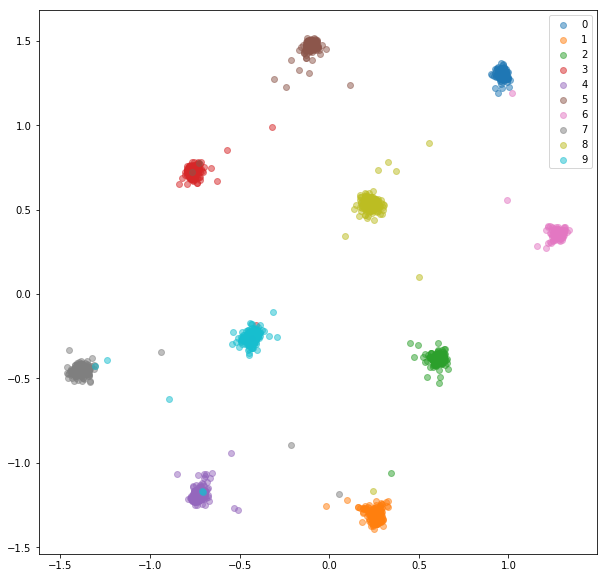
Ensemble de tests:
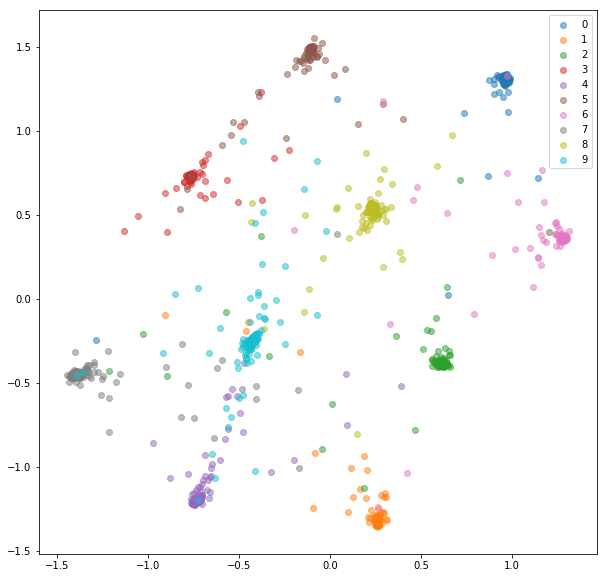
Les incorporations apprises sont bien mieux regroupées en classe.
Nous allons entraîner un réseau de triplet, qui prend une ancre, un exemple positif (de même classe qu'un ancre) et négatif (d'une classe différente d'une ancre). L'objectif est d'apprendre des intérêts de telle sorte que l'ancre est plus proche de l'exemple positif que de l'exemple négatif par une certaine valeur de marge.
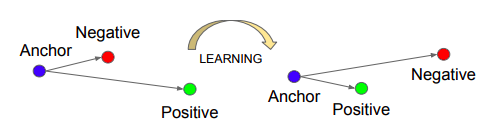Source: Schroff, Florian, Dmitry Kalenichenko et James Philbin. Facenet: Une intégration unifiée pour la reconnaissance faciale et le regroupement. CVPR 2015.
Perte du triplet :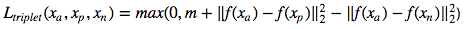 
La classe tripletmnist échantillonne un exemple positif et négatif pour chaque ancre possible.
Après 20 époques de formation, voici les intérêts que nous obtenons pour un ensemble de formation:
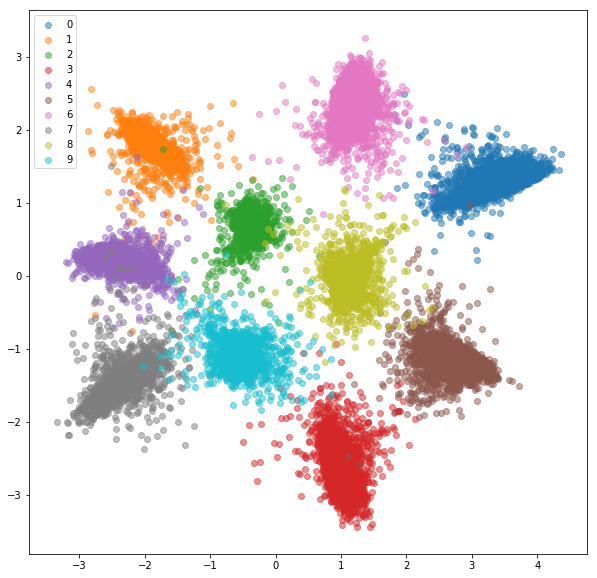
Ensemble de tests:
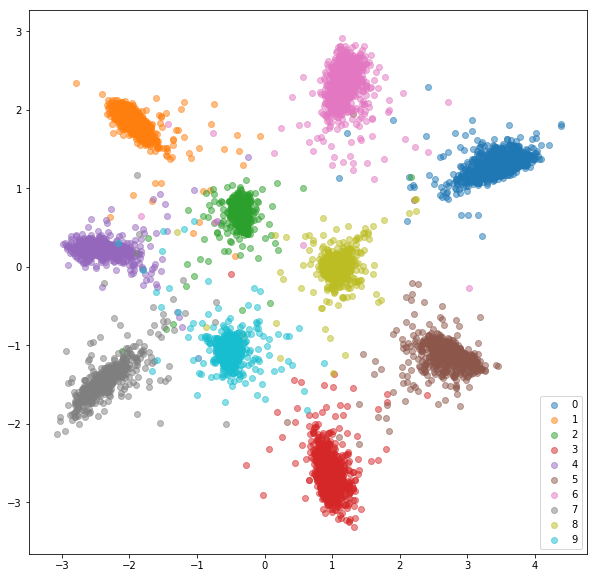
Les incorporations apprises ne sont pas aussi proches les unes des autres en classe que dans le cas du réseau siamois, mais ce n'est pas pour cela que nous les avons optimisés. Nous voulions que les intérêts soient plus proches des autres intégres de la même classe que des autres classes et nous pouvons voir que c'est là que la formation va.
Il y a quelques problèmes avec les réseaux siamois et triplet:
Pour traiter ces problèmes efficacement, nous allons nourrir un réseau avec des mini-lots standard comme nous l'avons fait pour la classification. La fonction de perte sera responsable de la sélection de paires dures et de triplets dans le mini-lot. Si nous nourrissons le réseau avec 16 images par 10 classes, nous pouvons traiter jusqu'à 159 * 160/2 = 12720 paires et 10 * 16 * 15/2 * (9 * 16) = 172800 triplés, par rapport à 80 paires et 53 triplés lors de l'implémentation précédente.
Habituellement, ce n'est pas la meilleure idée de traiter toutes les paires ou triplets possibles dans un mini-lot. Nous pouvons trouver des stratégies sur la façon de sélectionner les triplés dans [2] et [3].
Nous allons nourrir un réseau avec des mini-lots, comme nous l'avons fait pour le réseau de classification. Cette fois, nous utiliserons un échantillonnage spécial qui dégustera n_classes et n_s échantillons dans chaque classe, ce qui entraînera des mini lots de taille n_classes * n_s échantillons .
Pour chaque mini lot, les paires positives et négatives seront sélectionnées à l'aide d'étiquettes fournies.
MNIST est un ensemble de données assez facile et les incorporations des paires sélectionnées au hasard étaient déjà assez bonnes, nous ne voyons pas beaucoup d'amélioration ici.
TRAIN ANGRANDDINGS:
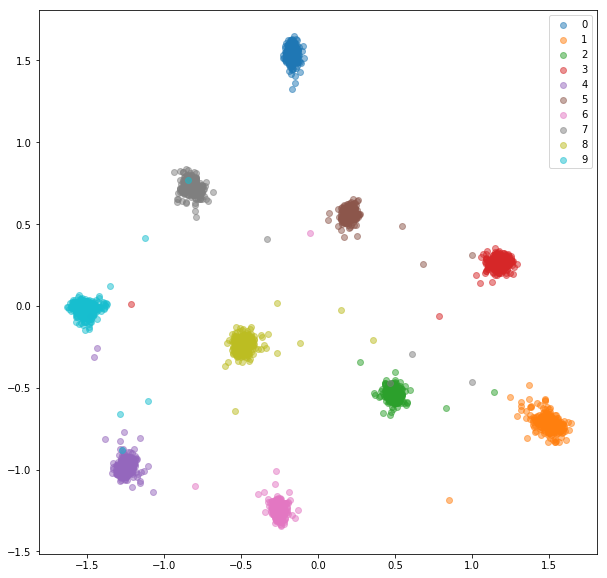
Tester les incorporations:
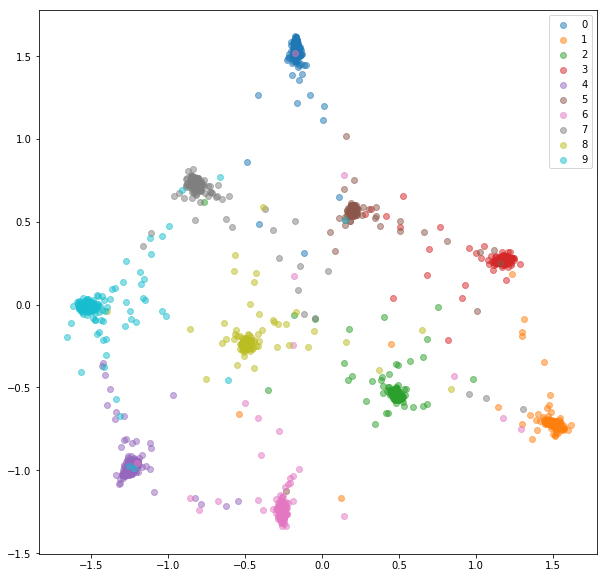
Nous allons nourrir un réseau avec des mini-lots comme avec la sélection des paires en ligne. Il y a quelques stratégies que nous pouvons utiliser pour la sélection des triplet donnant des étiquettes et des intérêts prévus:
La stratégie de sélection des triplet doit être choisie avec soin. Une mauvaise stratégie peut conduire à une formation inefficace ou, pire encore, à un effondrement de modélisation (toutes les incorporations finissent par avoir les mêmes valeurs).
Voici ce que nous avons obtenu avec des négatifs durs aléatoires pour chaque paire positive.
Ensemble de formation:
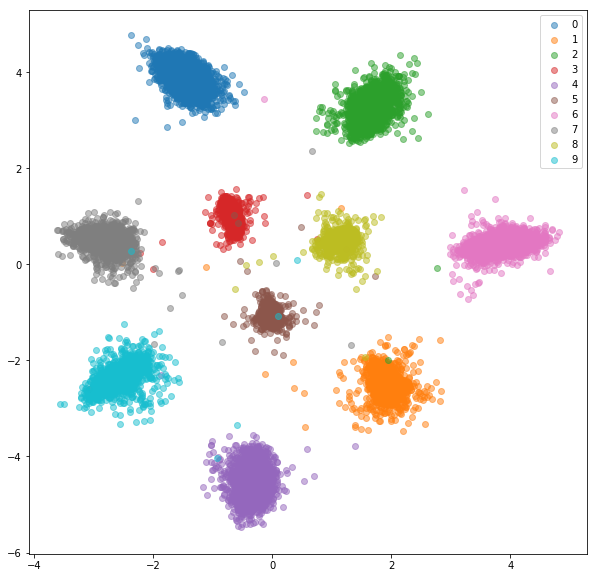
Ensemble de tests:
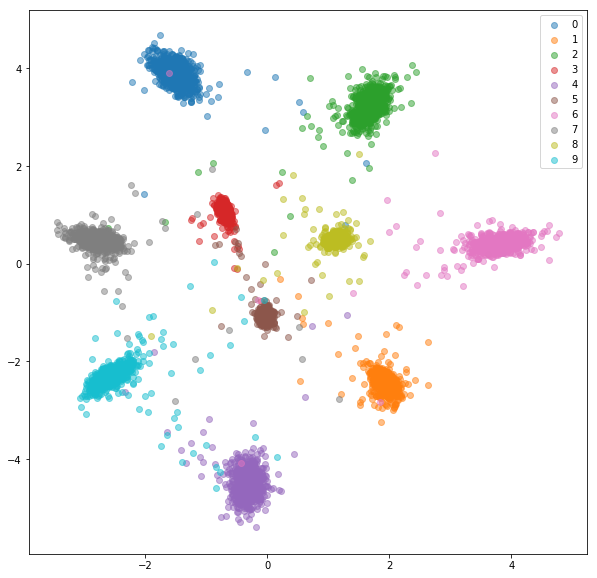
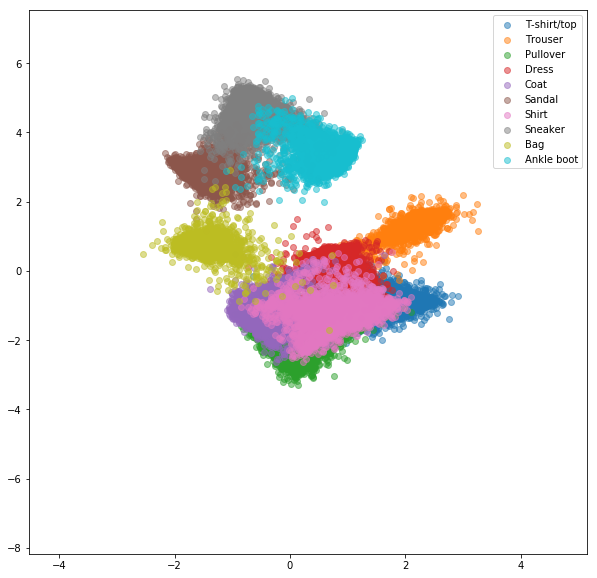
Des expériences similaires ont été menées pour un ensemble de données de mode de mode où les avantages de l'exploitation négative en ligne sont légèrement plus visibles. La même architecture de réseau exacte avec seulement des intérêts bidimensionnelles a été utilisée, ce qui n'est probablement pas assez complexe pour apprendre de bonnes intérêts. Des ensembles de données plus complexes avec des classes de nombres plus élevés devraient bénéficier encore plus de l'exploitation minière en ligne.
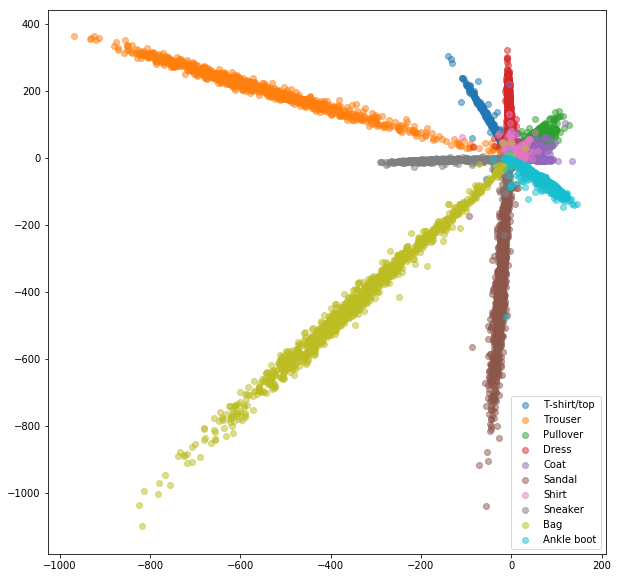
Réseau siamois avec des paires sélectionnées au hasard
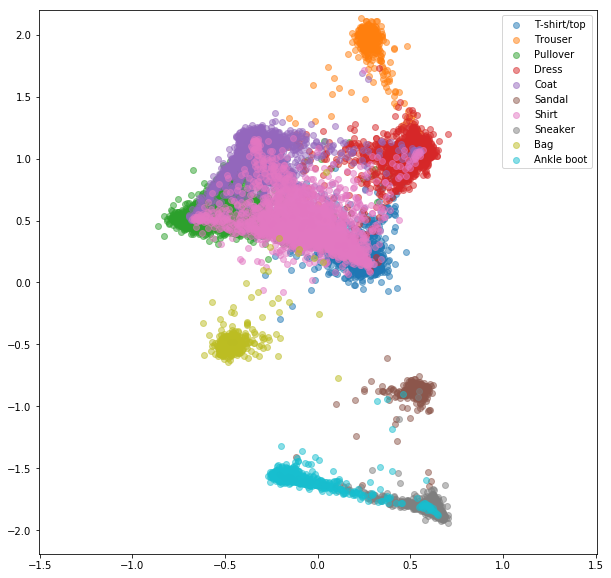
Perte contrastive en ligne avec l'exploitation négative
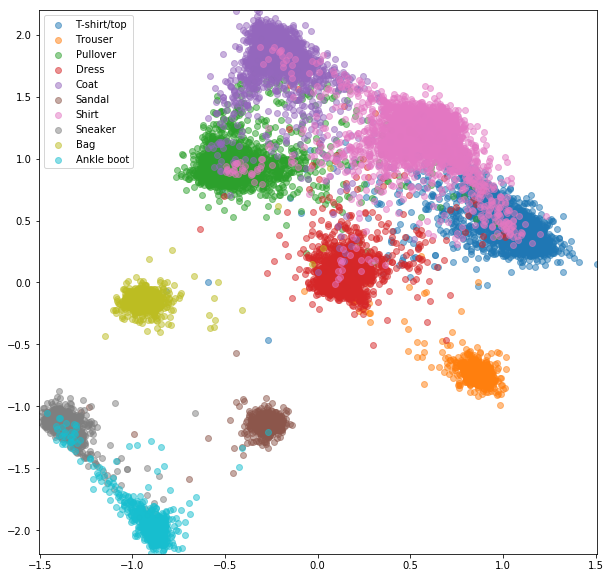
Réseau de triplet avec triplets aléatoires
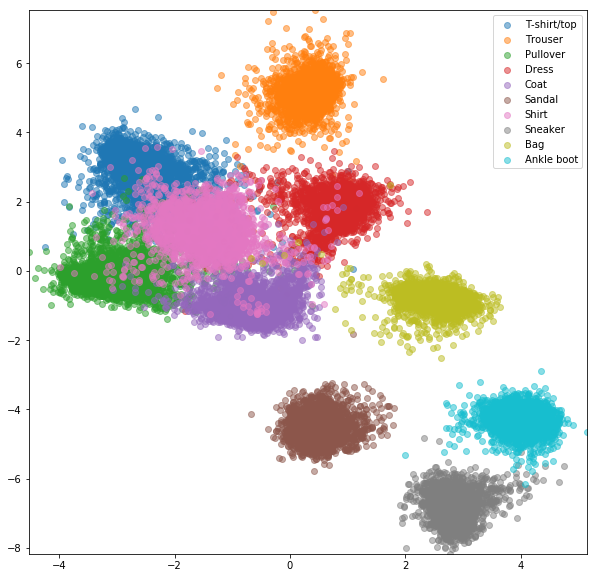
Perte de triplet en ligne avec une minière négative
[1] Raia Hadsell, Sumit Chopra, Yann LeCun, Réduction de la dimensionnalité en apprenant une cartographie invariante, CVPR 2006
[2] Schroff, Florian, Dmitry Kalenichenko et James Philbin. Facenet: Une intégration unifiée pour la reconnaissance faciale et le regroupement. CVPR 2015
[3] Alexander Hermans, Lucas Beyer, Bastian Leibe, en défense de la perte de triplet pour la réidentification des personnes, 2017
[4] Brandon Amos, Bartosz Ludwiczuk, Mahadev Satyanarayanan, Openface: une bibliothèque de reconnaissance faciale à usage général avec applications mobiles, 2016
[5] Yi Sun, Xiaogang Wang, Xiaoou Tang, Deep Learning Face Représentation par la vérification de l'identification conjointe, NIPS 2014
