TuoTuo 다운로드 TuoTuo 소스 코드 다운로드

TuoTuo

AI 소스 코드

Stable 0.2.7 release

다운로드

Tuotuo

Tuotuo 파이썬으로 작성된 주제 모델링 라이브러리. Tuotuo는 또한 6 개월 된 내 아들 인 귀여운 소년입니다.

설치

패키지 관리자 PIP를 사용하여 Tuotuo를 설치하십시오. 여기에서 PYPI 분포를 찾을 수 있습니다.

pip install TuoTuo --upgrade

용법

현재 라이브러리는 LDA (Latent Dirichlet 할당)를 통한 주제 모델링 만 지원합니다. 아시다시피, LDA는 Gibbs 샘플링 및 변형 추론을 사용하여 구현 될 수 있습니다. 수학적으로 더 정교함이므로 후자를 선택합니다.

5 개의 다른 주제와 40 개의 고유 단어에 걸쳐 사전 정의 된 Dirichlet 매개 변수를 기반으로 일부 문서를 생성하십시오.

 import torch as tr
from tuotuo . generator import doc_generator 

gen = doc_generator (
    M = 100 , 
    # we sample 100 documents 
    L = 20 , 
    # each document would contain 20 pre-defined words 
    topic_prior = tr . tensor ([ 1 , 1 , 1 , 1 , 1 ], dtype = tr . double )
    # we use a exchangable Dirichlet Distribution as our topic prior, 
    # that is a uniform distribution on 5 topics
)
train_docs = gen . generate_doc ()

교육 문서 양식 및 LDA의 변형 추론 매개 변수 교육

 from tuotuo . lda_model import LDASmoothed 
import matplotlib . pyplot as plt 

lda = LDASmoothed (
    num_topics = 5 , 
)

perplexes = lda . fit (
    train_docs ,
    sampling = False ,
    verbose = True , 
    return_perplexities = True ,
)
plt . plot ( perplexes )

= >= >= >= >= >= >= >= >
Topic Dirichlet Prior , Alpha
1

Exchangeable Word Dirichlet Prior , Eta 
1

Var Inf - Word Dirichlet prior , Lambda
( 5 , 40 )

Var Inf - Topic Dirichlet prior , Gamma
( 100 , 5 )

Init perplexity = 84.99592157507153
End perplexity = 45.96696541539976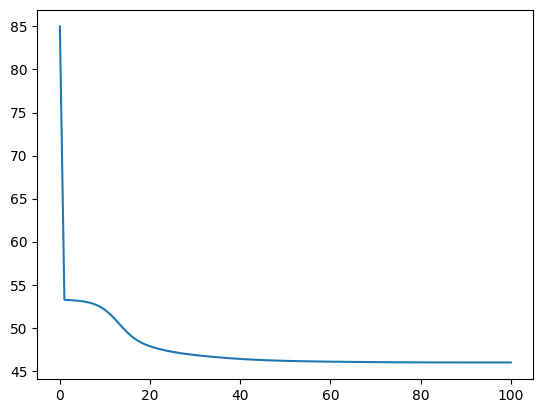

100 개 이상의 반복 이상의 당황

변형 추론 매개 변수에 따라 각 주제에 대한 상단 5 단어를 확인하십시오. $ lambda $

 for topic_index in range ( lda . _lambda_ . shape [ 0 ]):

    top5 = np . argsort ( lda . _lambda_ [ topic_index ,:],)[ - 5 :]
    print ( f"Topic { topic_index } " )
    for i , idx in enumerate ( top5 ):
        print ( f"Top { i + 1 } -> { lda . train_doc . idx_to_vocab [ idx ] } " )
    print ()

= >= >= >= >= >= >= >= >
Topic 0 
Top 1 -> physical
Top 2 -> quantum
Top 3 -> research
Top 4 -> scientst
Top 5 -> astrophysics

Topic 1
Top 1 -> divorce
Top 2 -> attorney
Top 3 -> court
Top 4 -> bankrupt
Top 5 -> contract

Topic 2
Top 1 -> content
Top 2 -> Craftsmanship
Top 3 -> concert
Top 4 -> asymmetrical
Top 5 -> Symmetrical

Topic 3
Top 1 -> recreation
Top 2 -> FIFA
Top 3 -> football
Top 4 -> Olympic
Top 5 -> athletics

Topic 4
Top 1 -> fever
Top 2 -> appetite
Top 3 -> contagious
Top 4 -> decongestant
Top 5 -> injection