min_span_tree_visualizer
1.0.0
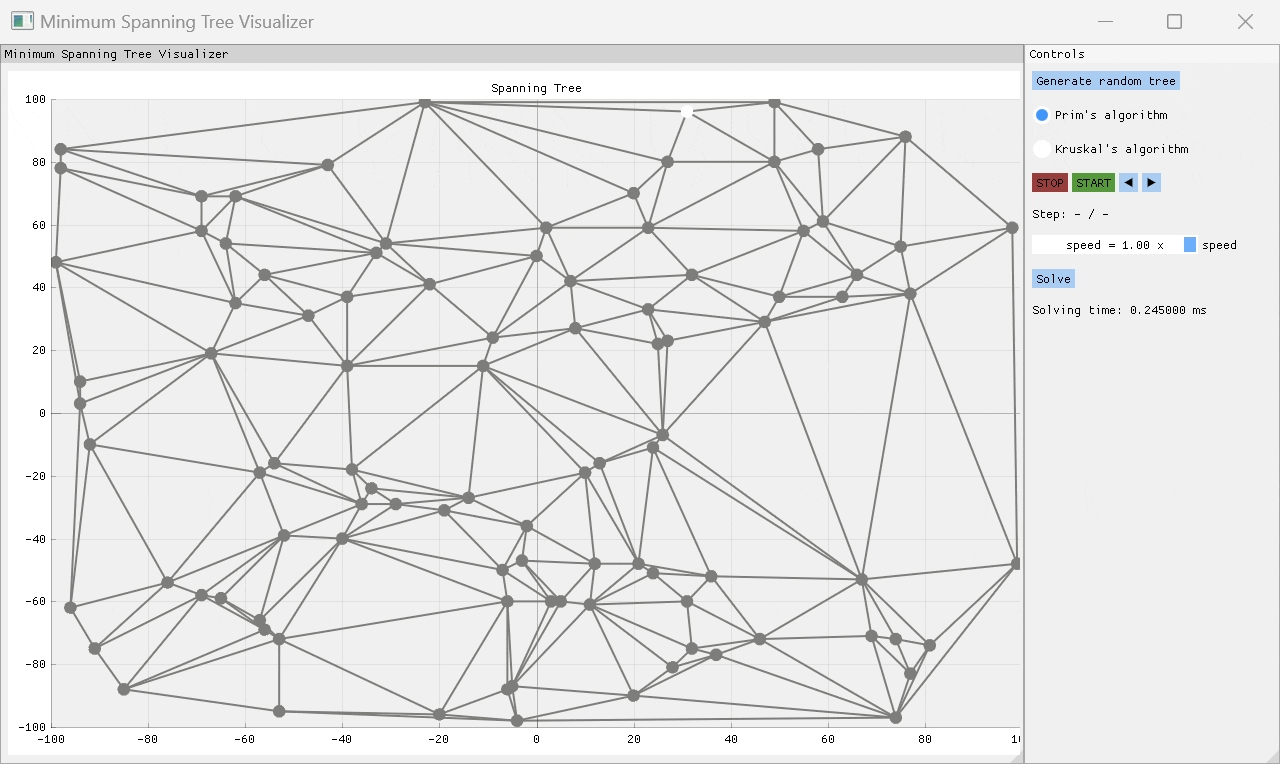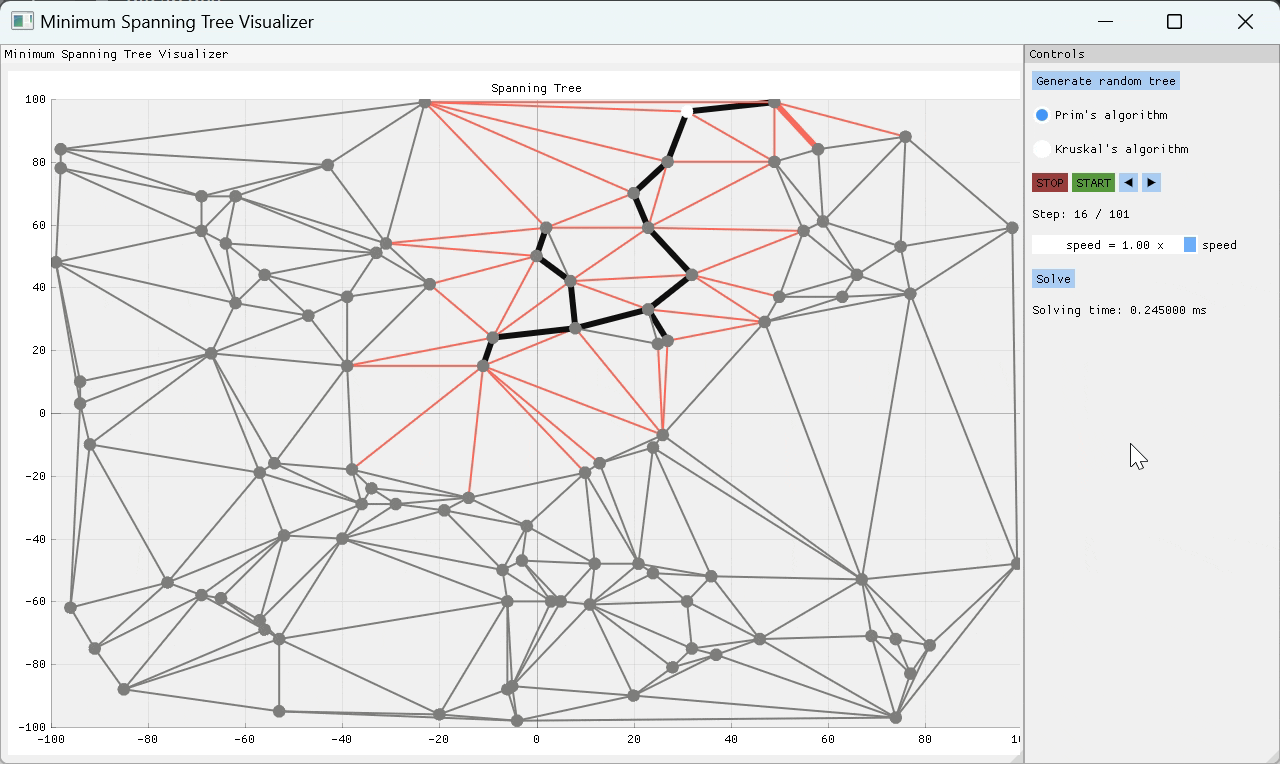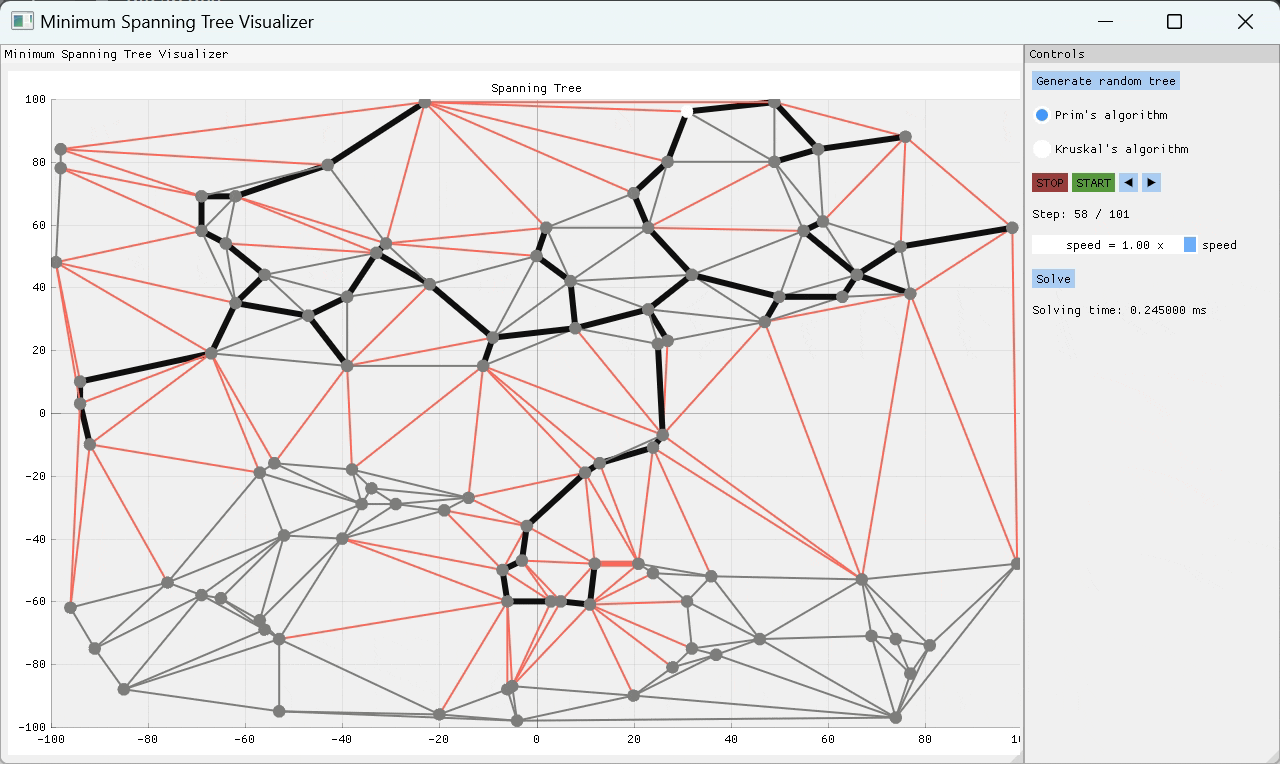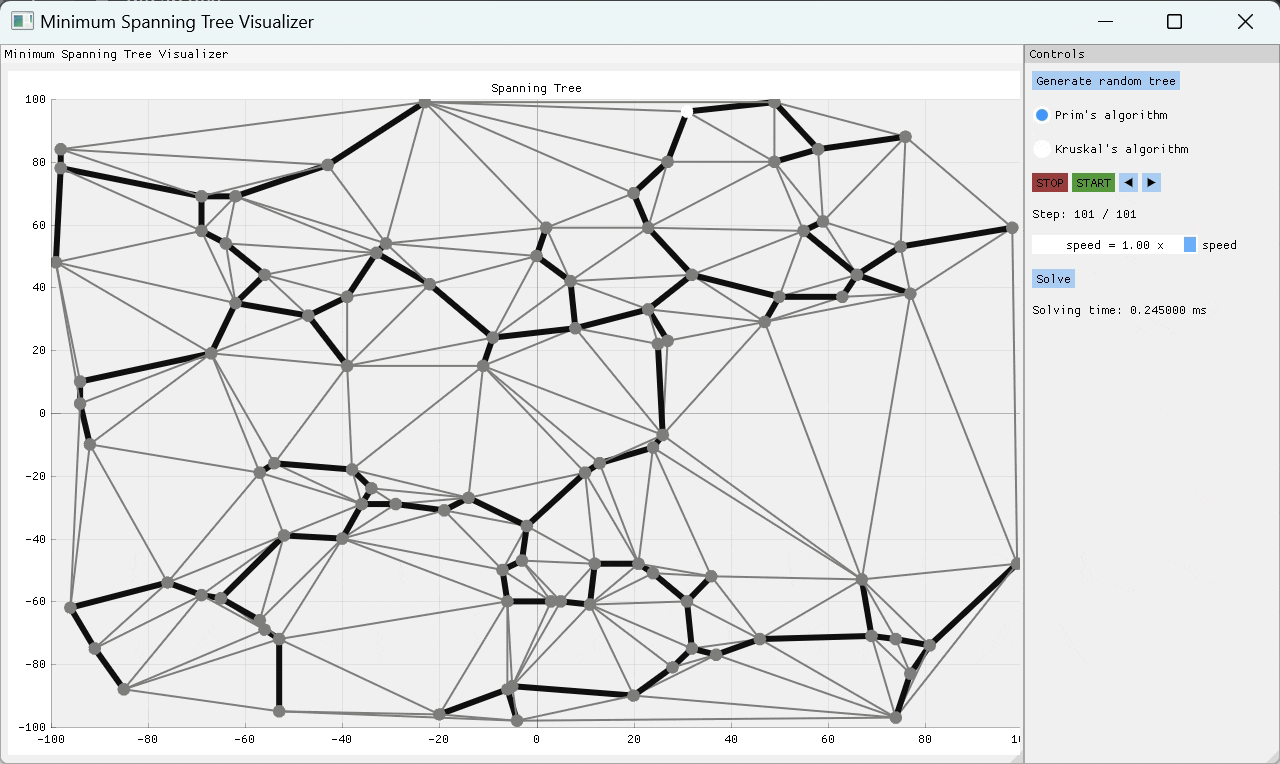
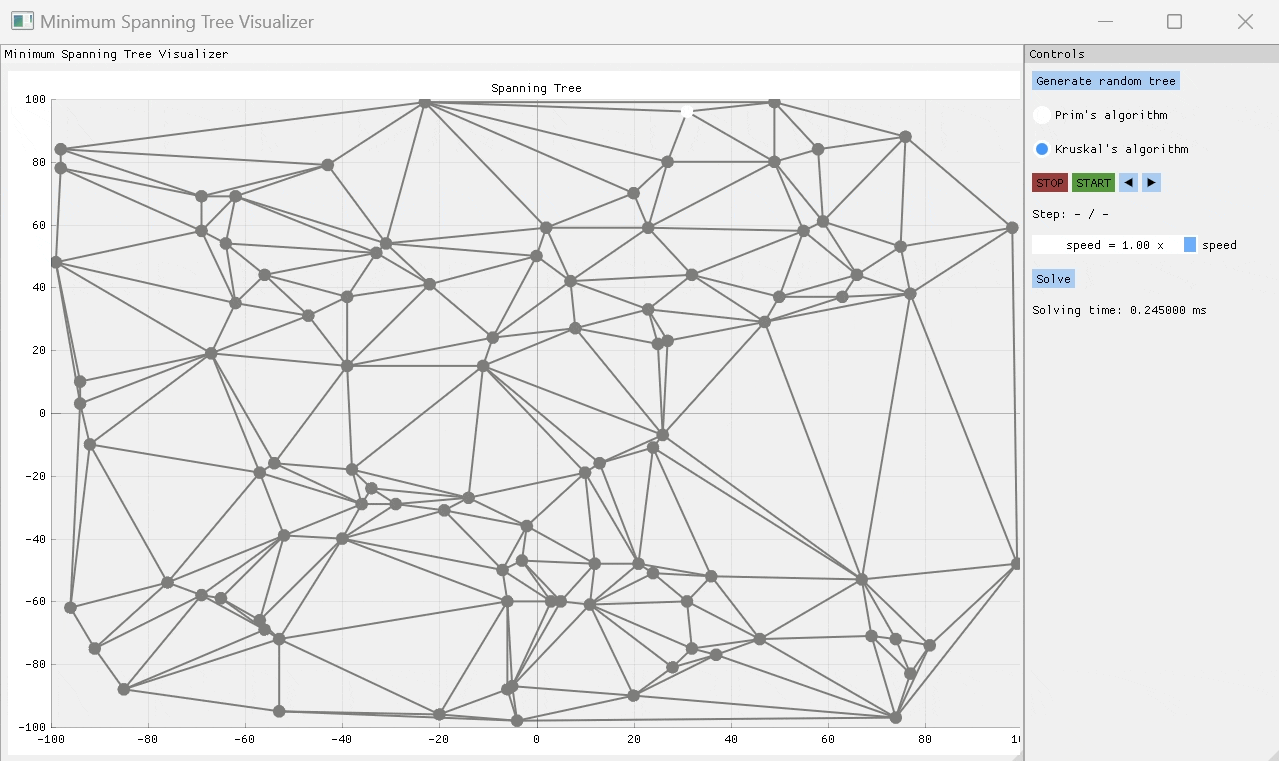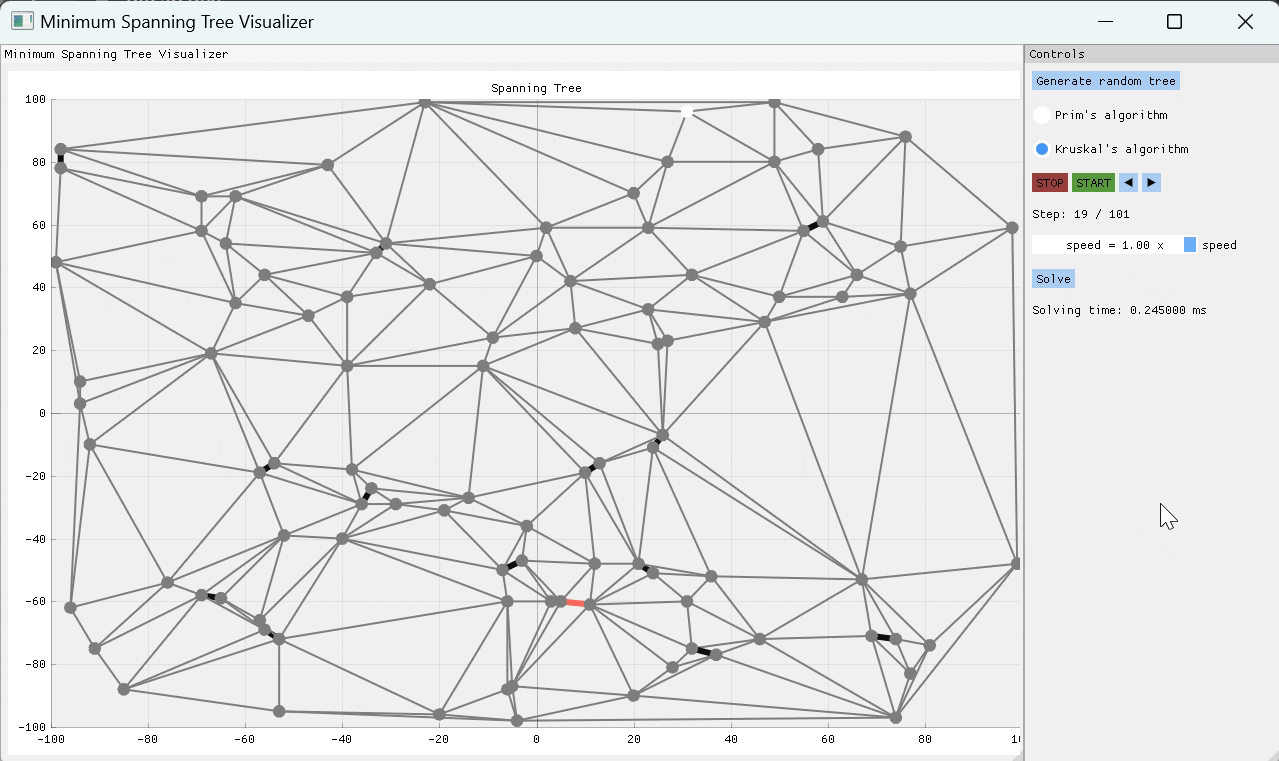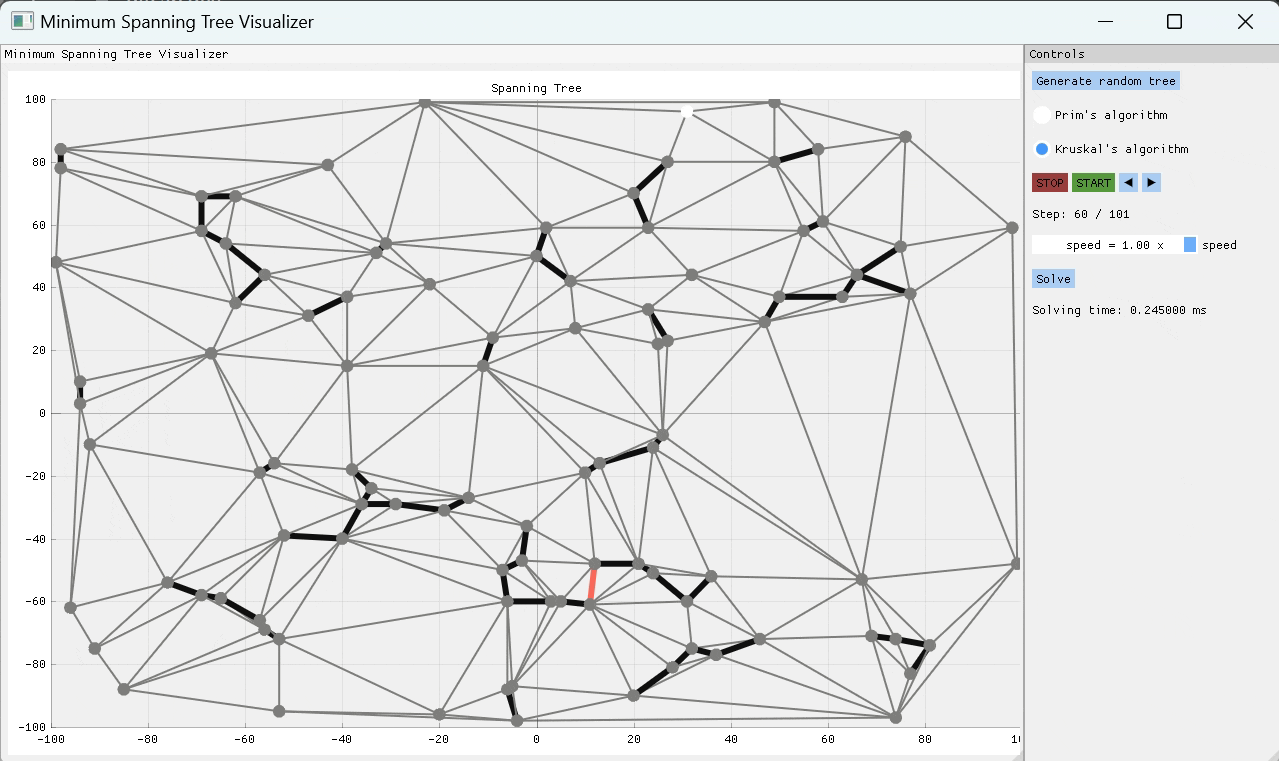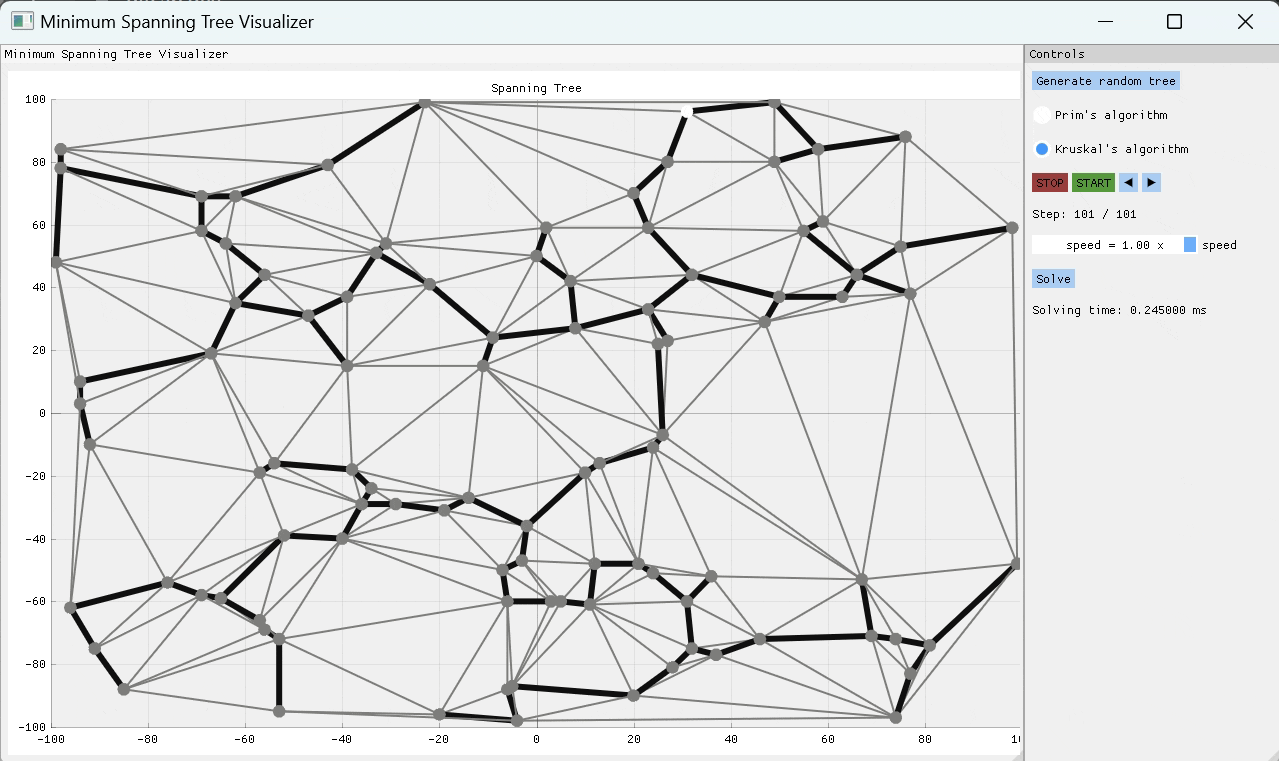
一個C ++項目，可視化兩個最常見的最小跨越樹（MST）算法的工作方式 - 主要是Kruskal和Prim的算法。該應用程序允許用戶隨機生成樹結構或從文件導入一個，然後選擇用於查找MST的算法。實現了有用的播放功能，以便用戶可以逐步查看算法如何到達最終解決方案。用戶可以逐步逐步解決算法求解過程，或者選擇播放速度並觀察其工作的魔術。
該項目的靈感來自以下兩個YouTube視頻，我認為嘗試在C ++中實現自己會很有趣：
Prim的算法動畫
Kruskal的算法動畫
在計算機科學中，圖是一個節點的集合，這些節點通過邊緣連接在一起，這些節點具有一些相關的權重。實際上，重量可能會使兩個節點之間的優勢有些物理含義，例如距離為米，時間為小時或成本為美元。一棵樹是沒有周期的圖形。 ie）以這樣的方式構造的，沒有可以遵循的邊路徑，這將使您可以回到與剩下的相同節點。因此，生成樹是某些圖的子圖，該圖是“跨越”或連接圖形的所有頂點的子圖。當選擇它以選擇具有最小重量時的邊緣的方式時，此生成樹也可以是“最小”生成樹（MST）。事實證明，MST在許多優化問題中非常有用，實際上，在為摩拉維亞市設計電力網絡時，發現了第一個MST算法。 1
雖然第一種解決此問題的算法是捷克數學家OtakarBorůvka發明的，但當今最受歡迎的兩種算法是Prim's和Kruskal的算法，這些算法是貪婪算法的例子，它們以略有不同的方式起作用。
PRIM的算法是一種貪婪的算象，一次通過檢查一些起始節點的所有外向邊緣，並將重量最低的邊緣添加到MST，從而一次構建MST One Edge。通過這種方式，MST是連續構建的，直到探索所有邊緣為止。
就像Prim的算法一次構建MST One Edge一樣，Kruskal的算法也這樣做，但是它可以通過以節點之間的許多不相交邊緣組開始，然後通過重量最小的邊緣將設置連接在一起，直到只有一組剩餘的Edges組為MST。
Chazelle的算法是找到MST的幾乎線性時間算法。
git clone到您的本地計算機。
從存儲庫的根目錄運行：
git clone https://github.com/Microsoft/vcpkg.git
完成後， cd到VCPKG文件夾並運行：
./bootstrap-vcpkg.sh
最後，運行：
./vcpkg integrate install
運行cd .. cd build ，然後運行cmake .. -DCMAKE_TOOLCHAIN_FILE=vcpkg/scripts/buildsystems/vcpkg.cmake 。如果一切順利，您將看到“構建文件已寫入...”消息。現在，您可以打開生成的“ MINIMUM_SPANNING_TREE_VISUALIZER”項目。
要運行測試，請右鍵單擊並“選擇為啟動項目”：
要運行測試，請右鍵單擊並“選擇為啟動項目”：
ojistémproblémuMinimálním（關於某些最小問題）↩
