min_span_tree_visualizer
1.0.0
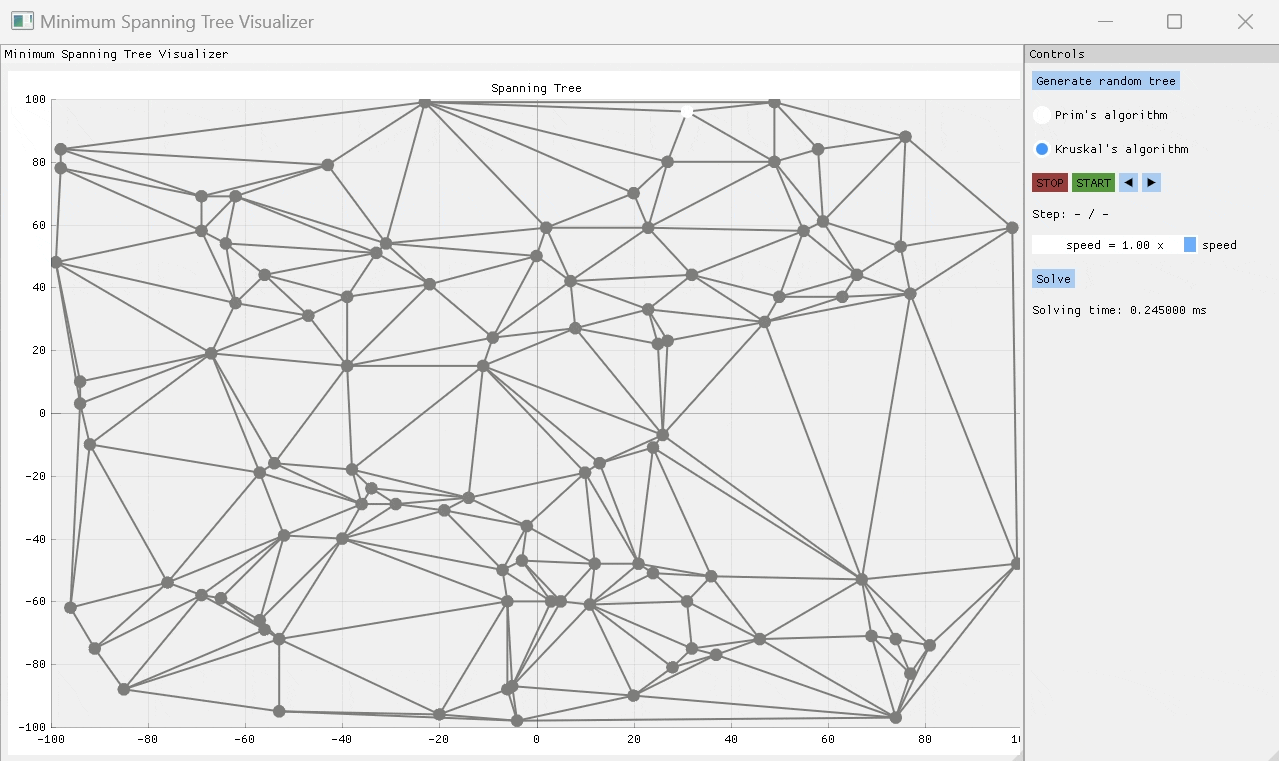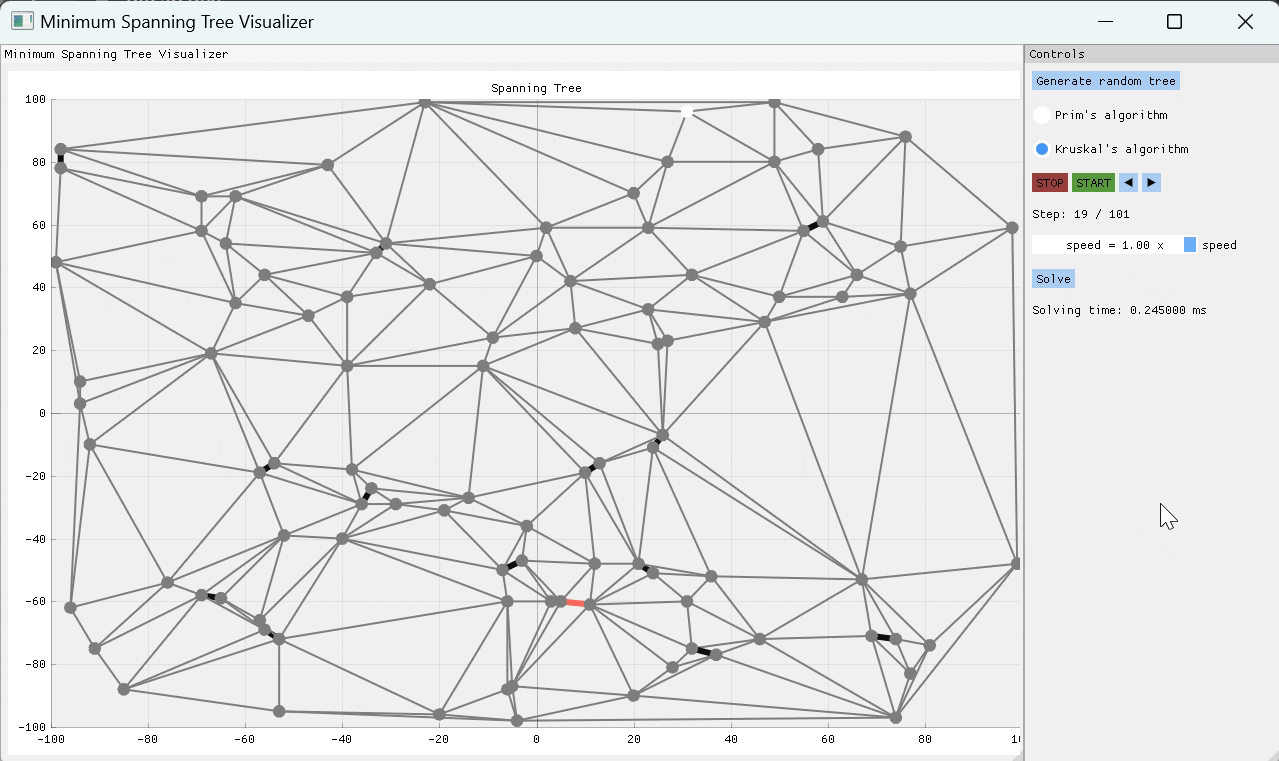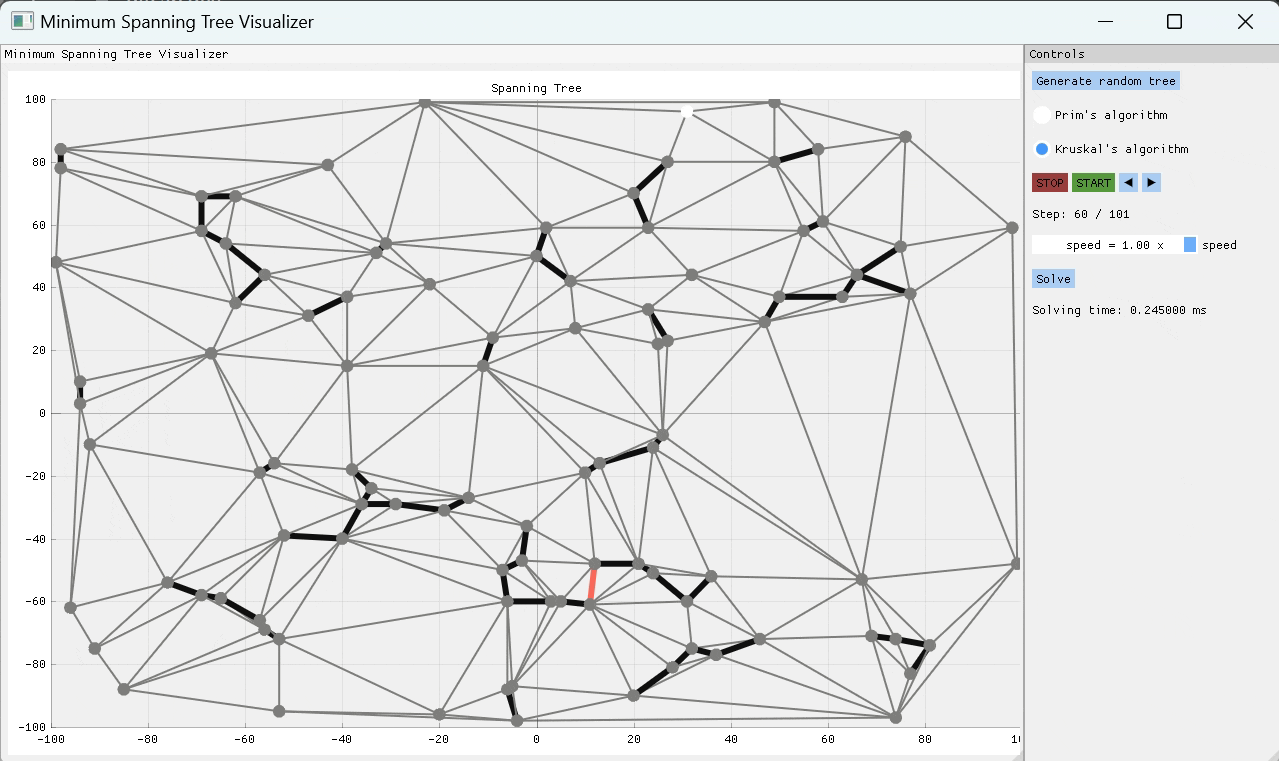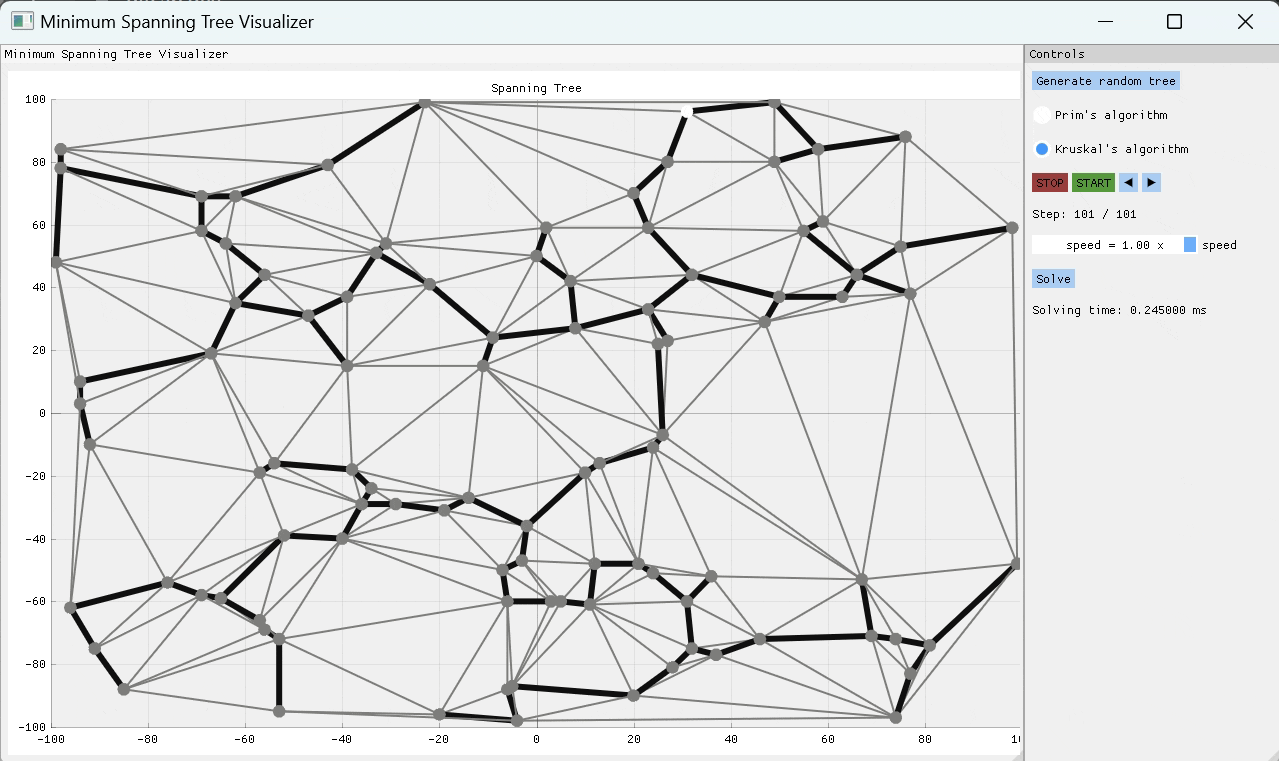
一个C ++项目，可视化两个最常见的最小跨越树（MST）算法的工作方式 - 主要是Kruskal和Prim的算法。该应用程序允许用户随机生成树结构或从文件导入一个，然后选择用于查找MST的算法。实现了有用的播放功能，以便用户可以逐步查看算法如何到达最终解决方案。用户可以逐步逐步解决算法求解过程，或者选择播放速度并观察其工作的魔术。
该项目的灵感来自以下两个YouTube视频，我认为尝试在C ++中实现自己会很有趣：
Prim的算法动画
Kruskal的算法动画
在计算机科学中，图是一个节点的集合，这些节点通过边缘连接在一起，这些节点具有一些相关的权重。实际上，重量可能会使两个节点之间的优势有些物理含义，例如距离为米，时间为小时或成本为美元。一棵树是没有周期的图形。 ie）以这样的方式构造的，没有可以遵循的边路径，这将使您可以回到与剩下的相同节点。因此，生成树是某些图的子图，该图是“跨越”或连接图形的所有顶点的子图。当选择它以选择具有最小重量时的边缘的方式时，此生成树也可以是“最小”生成树（MST）。事实证明，MST在许多优化问题中非常有用，实际上，在为摩拉维亚市设计电力网络时，发现了第一个MST算法。 1
虽然第一种解决此问题的算法是捷克数学家OtakarBorůvka发明的，但当今最受欢迎的两种算法是Prim's和Kruskal的算法，这些算法是贪婪算法的例子，它们以略有不同的方式起作用。
PRIM的算法是一种贪婪的算象，一次通过检查一些起始节点的所有外向边缘，并将重量最低的边缘添加到MST，从而一次构建MST One Edge。通过这种方式，MST是连续构建的，直到探索所有边缘为止。
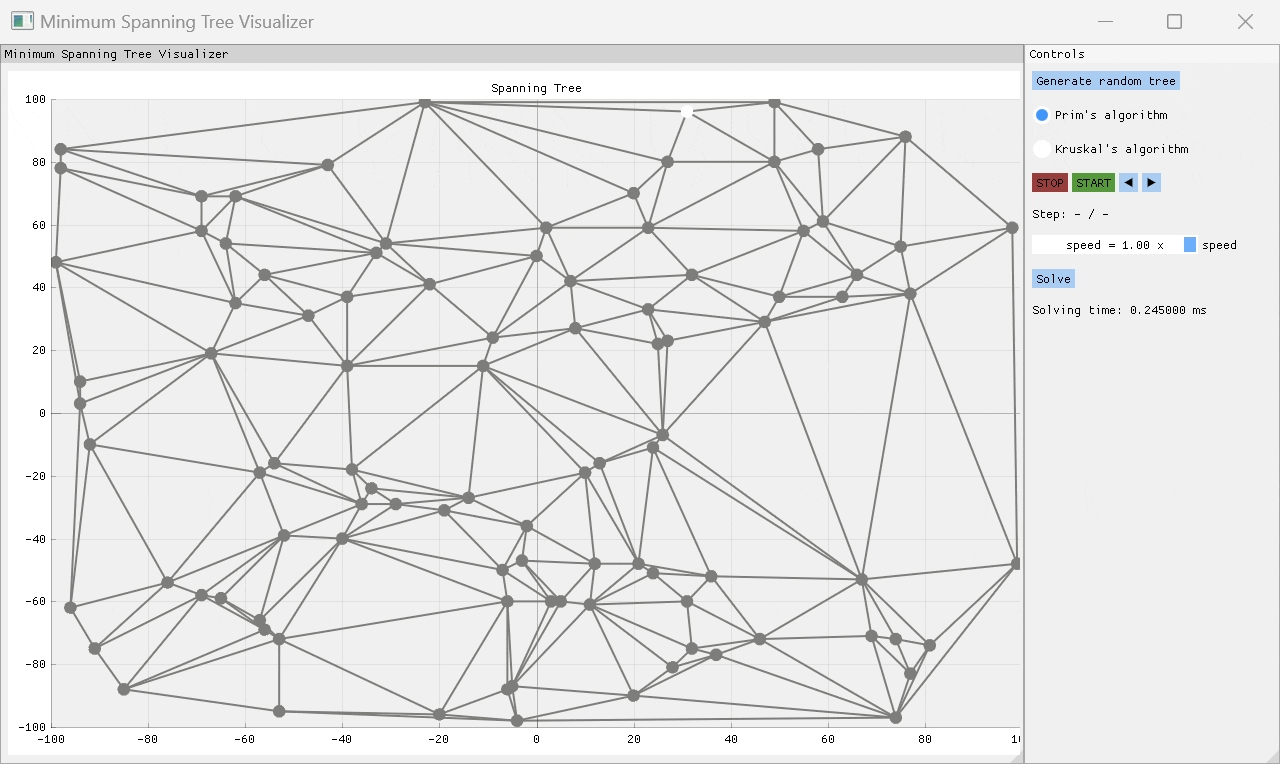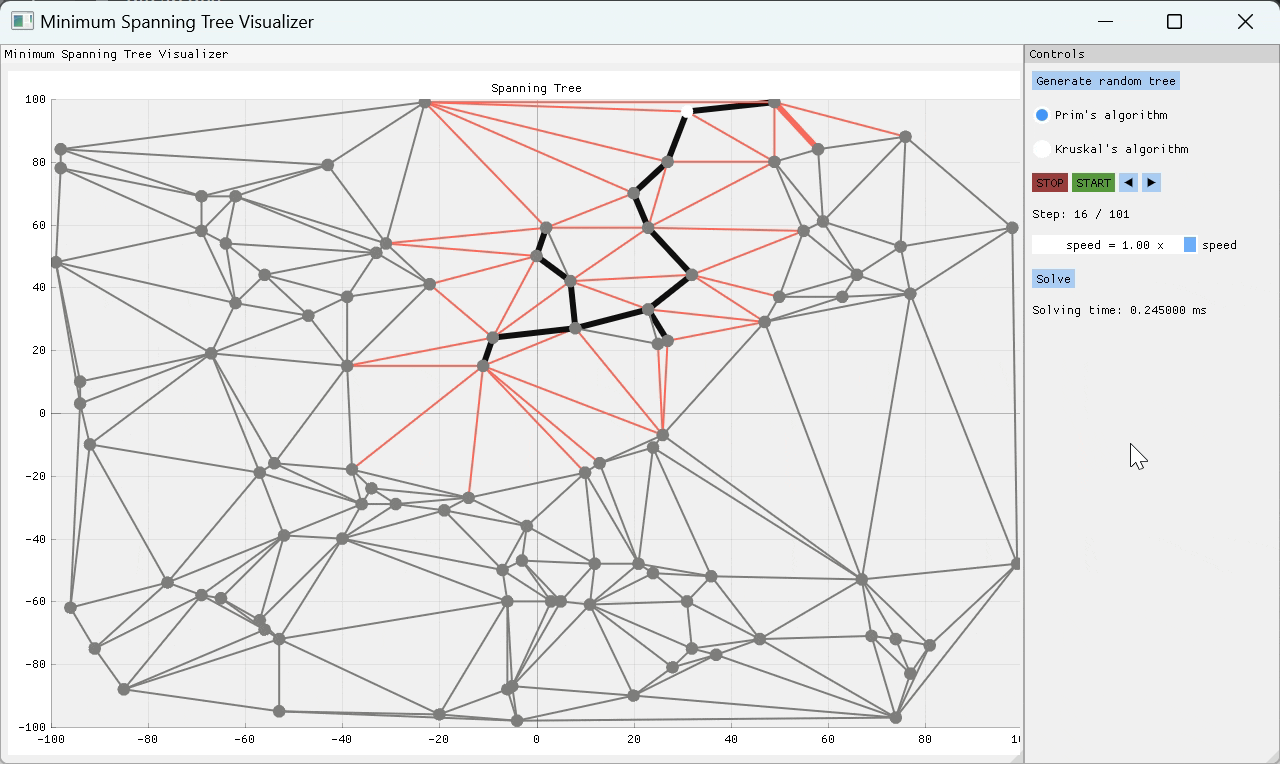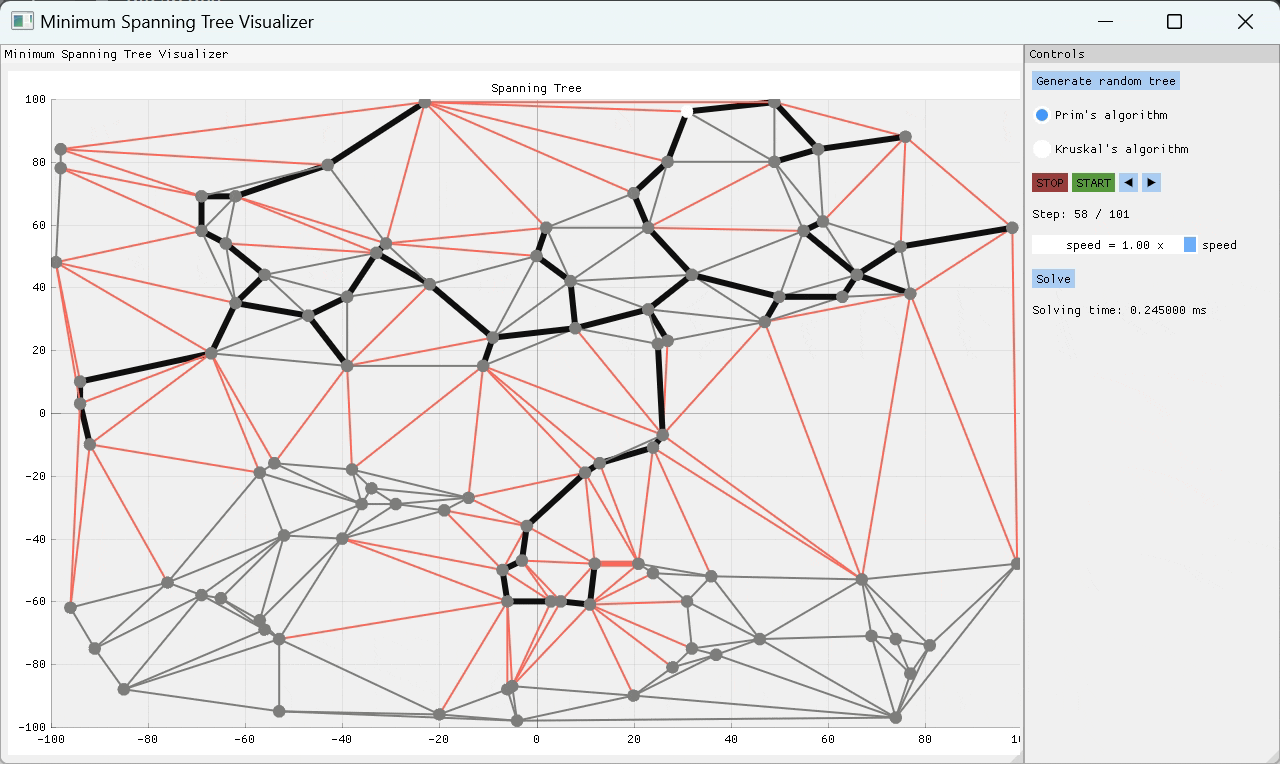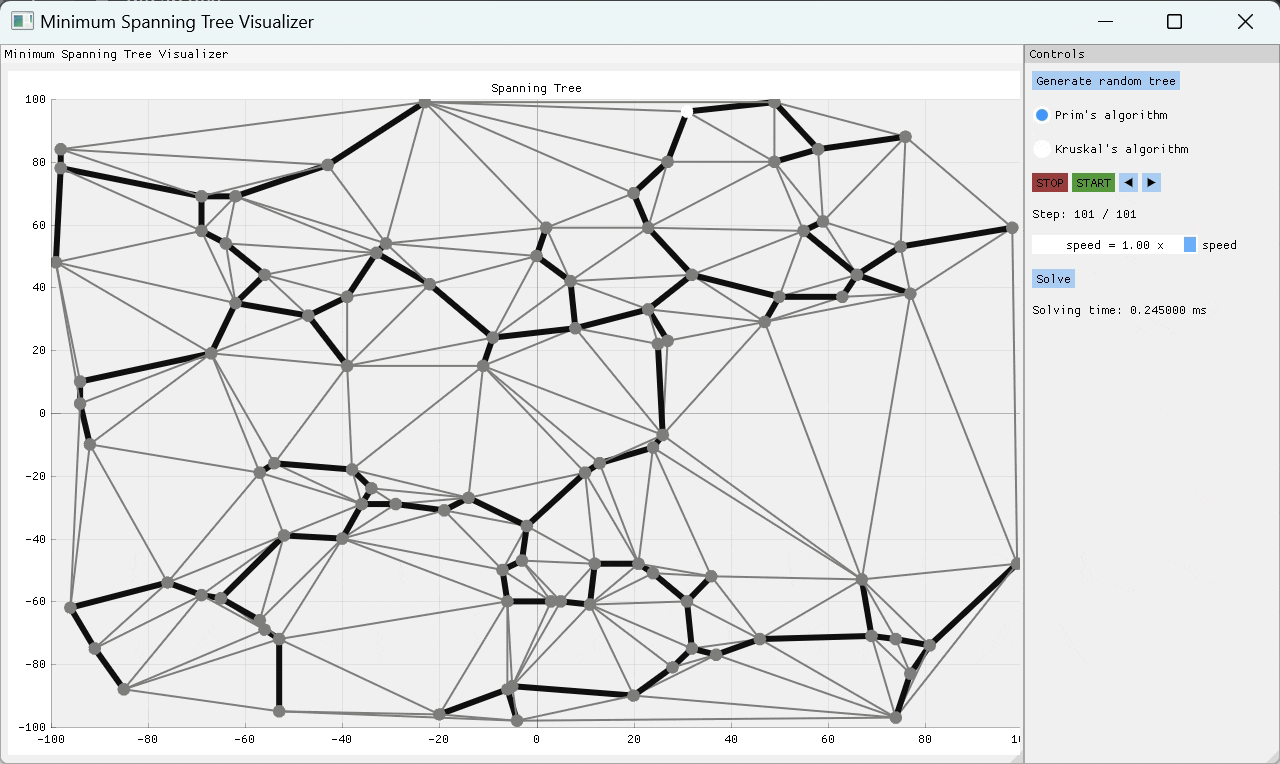
就像Prim的算法一次构建MST One Edge一样，Kruskal的算法也这样做，但是它可以通过以节点之间的许多不相交边缘组开始，然后通过重量最小的边缘将设置连接在一起，直到只有一组剩余的Edges组为MST。
Chazelle的算法是找到MST的几乎线性时间算法。
git clone到您的本地计算机。
从存储库的根目录运行：
git clone https://github.com/Microsoft/vcpkg.git
完成后， cd到VCPKG文件夹并运行：
./bootstrap-vcpkg.sh
最后，运行：
./vcpkg integrate install
运行cd .. cd build ，然后运行cmake .. -DCMAKE_TOOLCHAIN_FILE=vcpkg/scripts/buildsystems/vcpkg.cmake 。如果一切顺利，您将看到“构建文件已写入...”消息。现在，您可以打开生成的“ MINIMUM_SPANNING_TREE_VISUALIZER”项目。
要运行测试，请右键单击并“选择为启动项目”：
要运行测试，请右键单击并“选择为启动项目”：
ojistémproblémuMinimálním（关于某些最小问题）↩
