Uma equipe de ex-alunos da Tsinghua alcançou avanços matemáticos impressionantes com a ajuda da IA! O LeanAgent que desenvolveram, um assistente de IA com capacidades de aprendizagem ao longo da vida, provou com sucesso 162 teoremas matemáticos anteriormente não resolvidos e até resolveu o problema formal da conjectura polinomial de Freiman-Ruzsa proposta por Terence Tao. Isto não só demonstra o enorme potencial da IA na investigação científica básica, mas também marca uma inovação nos métodos de investigação matemática. Os editores de downcodes lhe darão uma compreensão profunda deste desenvolvimento emocionante e da inovação tecnológica por trás do LeanAgent.
Nas últimas notícias sensacionais do mundo da matemática, um grupo de ex-alunos da Universidade Tsinghua usou o poder da IA para provar com sucesso 162 teoremas matemáticos que ninguém havia conseguido resolver antes. O que é ainda mais surpreendente é que este agente chamado LeanAgent realmente superou o problema de formalização da conjectura polinomial de Freiman-Ruzsa de Terence Tero. Isso nos faz lamentar que os métodos de pesquisa da ciência básica tenham sido completamente transformados pela IA.
Como todos sabemos, embora os modelos de linguagem atuais (LLM) sejam legais, a maioria deles ainda é estática e não pode aprender novos conhecimentos online. É ainda mais difícil provar teoremas matemáticos avançados. No entanto, o LeanAgent, desenvolvido em conjunto por equipes de pesquisa da Caltech, da Universidade de Stanford e da Universidade de Washington, é um assistente de IA com capacidades de aprendizagem ao longo da vida que pode aprender e provar teoremas continuamente.
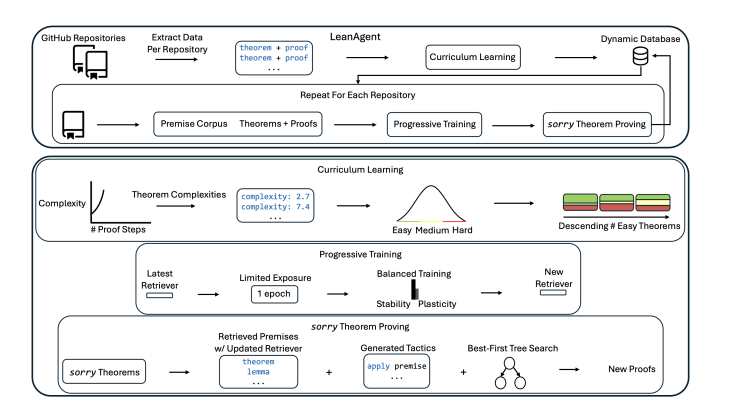
O LeanAgent responde a diferentes dificuldades matemáticas através de caminhos de aprendizagem cuidadosamente concebidos e utiliza uma base de dados dinâmica para gerir um fluxo contínuo de conhecimento matemático para garantir que não se esquece das competências que já domina ao aprender novos conhecimentos. Experimentos mostram que ele provou com sucesso 162 teoremas matemáticos que ninguém foi capaz de resolver antes de 23 bibliotecas de código Lean diferentes, e seu desempenho é 11 vezes maior do que o dos grandes modelos tradicionais.
Esses teoremas cobrem muitas áreas da matemática superior, incluindo problemas difíceis como álgebra abstrata e topologia algébrica. O LeanAgent não só é capaz de começar com conceitos simples e abordar gradualmente tópicos complexos, como também demonstra excelente desempenho em termos de estabilidade e migração reversa.
No entanto, o desafio de Terence Tao ainda faz com que a IA se sinta impotente. Embora os provadores interativos de teoremas (ITPs), como o Lean, desempenhem um papel importante na formalização e verificação de provas matemáticas, o processo de construção de tais provas é muitas vezes complexo e demorado, exigindo etapas meticulosas e extensas bibliotecas de códigos matemáticos. Grandes modelos avançados como o1 e Claude também estão sujeitos a erros quando confrontados com provas informais, o que destaca as deficiências do LLM na precisão e confiabilidade das provas matemáticas.
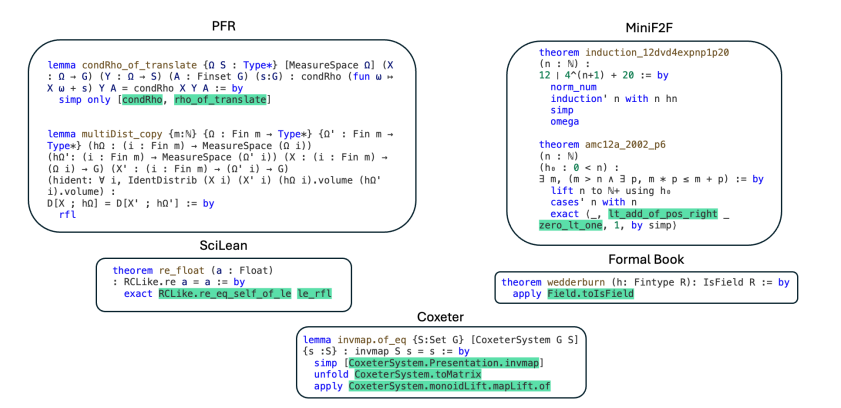
Pesquisas anteriores tentaram usar o LLM para gerar etapas de prova completas, como o LeanDojo, que é um provador de teoremas criado pelo treinamento de um grande modelo em um conjunto de dados específico. No entanto, os dados para provas formais de teoremas são extremamente escassos, limitando a ampla aplicabilidade desta abordagem. Outro projeto, ReProver, é um modelo otimizado para a biblioteca de códigos de prova de teorema Lean mathlib4. Embora cubra mais de 100.000 teoremas e definições matemáticas formais, é limitado ao escopo da matemática de graduação, por isso não tem um bom desempenho quando enfrenta problemas mais complexos. problemas.
Vale a pena notar que a natureza dinâmica da investigação matemática traz maiores desafios à IA. Os matemáticos geralmente trabalham em vários projetos ao mesmo tempo ou alternadamente. Por exemplo, Terence Tao está avançando em várias áreas de pesquisa ao mesmo tempo, incluindo conjecturas PFR e média simétrica de números reais. Estes exemplos mostram uma deficiência fundamental dos atuais métodos de prova de teoremas de IA: a falta de um sistema de IA que possa aprender e melhorar de forma adaptativa em diferentes campos matemáticos, especialmente quando os dados Lean são limitados.
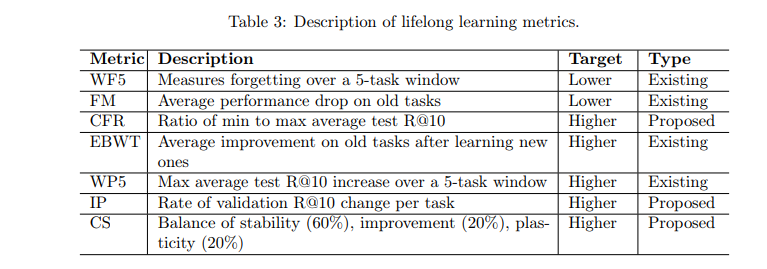
É por isso que a equipe do LeanDojo criou o LeanAgent, uma nova estrutura de aprendizagem ao longo da vida projetada para resolver os desafios acima. O fluxo de trabalho do LeanAgent inclui a derivação da complexidade de teoremas para formular cursos de aprendizagem, equilibrando estabilidade e flexibilidade no processo de aprendizagem por meio de treinamento progressivo e utilizando a melhor pesquisa em árvore para encontrar teoremas ainda não comprovados.
LeanAgent trabalha com qualquer modelo grande para melhorar suas capacidades de generalização através de “recuperação”. Sua inovação reside no uso de um banco de dados dinâmico personalizado para gerenciar o conhecimento matemático em constante expansão e uma estratégia de aprendizagem de curso baseada na estrutura de prova Lean para ajudar a aprender conteúdos matemáticos mais complexos.
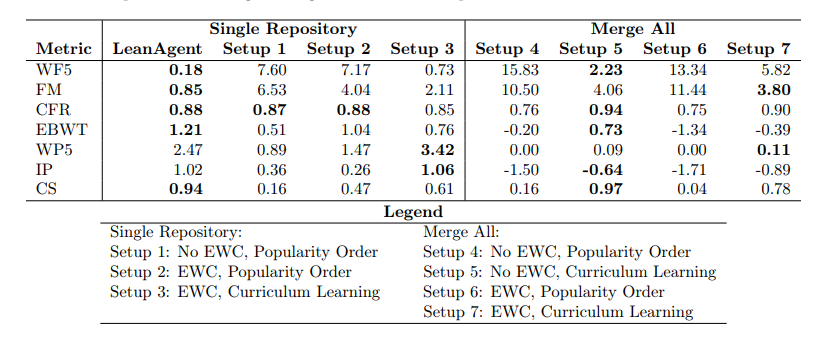
Para lidar com o problema catastrófico do esquecimento da IA, os pesquisadores adotaram um método de treinamento progressivo para permitir que o LeanAgent se adaptasse continuamente a novos conhecimentos matemáticos sem esquecer o aprendizado anterior. Este processo envolve treinamento incremental em cada novo conjunto de dados, garantindo um equilíbrio ideal entre estabilidade e flexibilidade.
Através deste tipo de treinamento progressivo, o LeanAgent tem excelente desempenho na prova de teoremas, provando com sucesso 162 problemas difíceis que não foram resolvidos por humanos, especialmente em desafiar teoremas de álgebra abstrata e topologia algébrica. Sua capacidade de provar novos teoremas é 11 vezes maior que a do ReProver estático, mantendo sua capacidade de provar teoremas conhecidos.
O LeanAgent mostra as características do aprendizado progressivo durante o processo de prova de teoremas, transitando gradativamente de teoremas simples para teoremas mais complexos, comprovando sua profundidade no domínio do conhecimento matemático. Por exemplo, demonstra uma compreensão profunda da matemática ao provar teoremas fundamentais da estrutura algébrica relacionados à teoria dos grupos e à teoria dos anéis. No geral, o LeanAgent traz perspectivas interessantes para a comunidade matemática com seus poderosos recursos de aprendizado e melhoria contínua!
Endereço do artigo: https://arxiv.org/pdf/2410.06209
O surgimento do LeanAgent indica que a IA desempenhará um papel cada vez mais importante no campo da investigação matemática, e poderá haver mais casos no futuro que utilizem o poder da IA para resolver problemas matemáticos complexos. Isto, sem dúvida, abre uma nova direção para a pesquisa matemática e também fornece novas ideias e métodos para exploração em outros campos científicos. Ansiosa por mais resultados surpreendentes no futuro!