清華大学の卒業生のチームは、AI の助けを借りて素晴らしい数学的進歩を達成しました。彼らが開発した生涯学習機能を備えた AI アシスタントである LeanAgent は、これまで未解決だった 162 個の数学定理の証明に成功し、テレンス・タオが提案した多項式フライマン・ルザ予想の形式問題も解決しました。これは、基礎科学研究における AI の大きな可能性を実証するだけでなく、数学的研究手法における革新を示しています。 Downcodes エディターを使用すると、このエキサイティングな開発と LeanAgent の背後にある技術革新を深く理解できます。
数学界における最新のセンセーショナルなニュースでは、清華大学の卒業生グループが AI の力を利用して、これまで誰も解決できなかった 162 の数学定理の証明に成功しました。さらに驚くべきことは、この LeanAgent というエージェントが、テレンス・テロの多項式フライマン・ルザ予想の形式化問題を実際に克服したということです。
誰もが知っているように、現在の言語モデル (LLM) は優れていますが、そのほとんどは依然として静的であり、オンラインで新しい知識を学習することはできません。高度な数学定理を証明することはさらに困難です。しかし、カリフォルニア工科大学、スタンフォード大学、ワシントン大学の研究チームが共同開発した LeanAgent は、定理を継続的に学習して証明できる生涯学習機能を備えた AI アシスタントです。
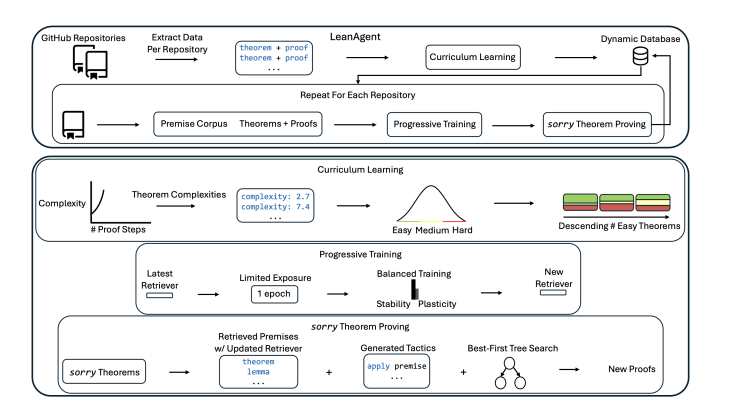
LeanAgent は、慎重に設計された学習パスを通じてさまざまな数学的困難に対応し、動的なデータベースを使用して数学的知識の継続的な流れを管理し、新しい知識を学習する際にすでに習得したスキルを忘れないようにします。実験の結果、23 の異なるリーン コード ライブラリから、これまで誰も解決できなかった 162 の数学定理を証明することに成功し、そのパフォーマンスは従来の大規模モデルの 11 倍であることが示されています。本当に素晴らしいです。
これらの定理は、抽象代数や代数トポロジーなどの難しい問題を含む、高等数学の多くの分野をカバーしています。 LeanAgent は、単純な概念から始めて徐々に複雑なトピックに取り組むことができるだけでなく、安定性と逆移行の点でも優れたパフォーマンスを発揮します。
しかし、テレンス・タオの挑戦は依然として AI を無力に感じさせます。 Lean などのインタラクティブ定理証明者 (ITP) は数学的証明の形式化と検証において重要な役割を果たしますが、そのような証明を構築するプロセスは多くの場合複雑で時間がかかり、細心の手順と広範な数学コード ライブラリが必要です。 o1 や Claude のような高度な大規模モデルも、非公式な証明に直面した場合にエラーが発生しやすく、数学的証明の精度と信頼性における LLM の欠点が浮き彫りになります。
過去の研究では、特定のデータセットで大規模なモデルをトレーニングすることによって作成された定理証明器である LeanDojo など、LLM を使用して完全な証明ステップを生成することが試みられました。ただし、形式的な定理証明のデータは非常に不足しており、このアプローチの広範囲にわたる適用性は制限されています。もう 1 つのプロジェクトである ReProver は、リーン定理証明コード ライブラリ mathlib4 用に最適化されたモデルです。これは 100,000 を超える正式な数学定理と定義をカバーしていますが、学部数学の範囲に限定されているため、より複雑な問題に直面した場合にはうまく機能しません。問題は良い。
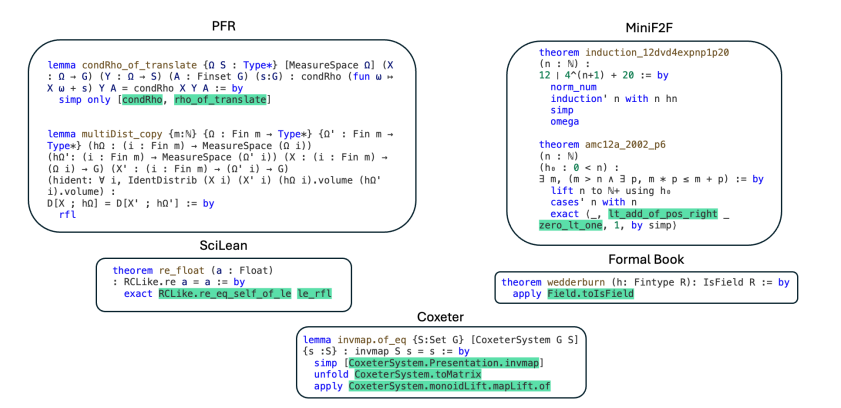
数学研究の動的な性質が AI に大きな課題をもたらすことは注目に値します。数学者は通常、複数のプロジェクトに同時にまたは交互に取り組んでいます。たとえば、テレンス・タオ氏は、PFR 予想や実数対称平均など、複数の研究分野を同時に進めています。これらの例は、現在の AI 定理証明方法の重大な欠点を示しています。それは、特にリーン データが限られている場合に、さまざまな数学分野で適応的に学習して改善できる AI システムが欠如していることです。
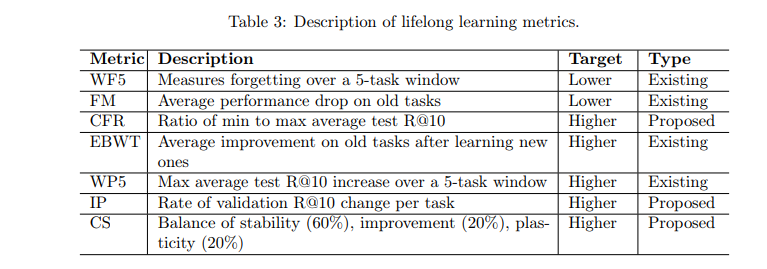
そのため、LeanDojo のチームは、上記の課題を解決するために設計された新しい生涯学習フレームワークである LeanAgent を作成しました。 LeanAgent のワークフローには、学習コースを策定するための定理の複雑さの導出、プログレッシブ トレーニングによる学習プロセスの安定性と柔軟性のバランス、まだ証明されていない定理を見つけるための最良優先ツリー検索の利用が含まれます。
LeanAgent はあらゆる大規模モデルと連携して、「検索」を通じて汎化機能を向上させます。その革新性は、拡大し続ける数学的知識を管理するカスタム動的データベースの使用と、より複雑な数学的内容の学習を支援する無駄のない証明構造に基づくコース学習戦略にあります。
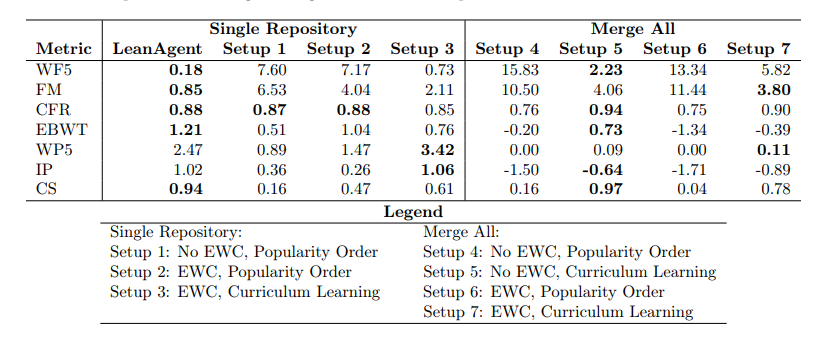
AI の壊滅的な忘却問題に対処するために、研究者らは、LeanAgent が以前の学習を忘れることなく新しい数学的知識に継続的に適応できるようにするための進歩的なトレーニング方法を採用しました。このプロセスには、新しいデータセットごとに増分トレーニングが含まれ、安定性と柔軟性の最適なバランスが確保されます。
このような進歩的なトレーニングを通じて、LeanAgent は定理の証明において優れたパフォーマンスを発揮し、特に抽象代数および代数トポロジーの難解な定理において、人間によって解決されていない 162 の困難な問題の証明に成功しました。既知の定理を証明する能力を維持しながら、新しい定理を証明する能力は静的 ReProver の 11 倍です。
LeanAgent は、定理証明プロセス中に漸進的学習の特徴を示し、単純な定理からより複雑な定理に徐々に移行し、数学的知識の習得における深さを証明します。たとえば、群理論や環理論に関連する基本的な代数構造定理を証明することで、数学の深い理解を示します。全体として、LeanAgent は、強力な継続学習および改善機能により、数学コミュニティに刺激的な展望をもたらします。
論文アドレス: https://arxiv.org/pdf/2410.06209
LeanAgent の登場は、AI が数学研究の分野でますます重要な役割を果たすことを示しており、将来的には AI の力を利用して複雑な数学的問題を解決するケースがさらに増える可能性があります。 これは間違いなく数学研究に新たな方向性を切り開き、他の科学分野の探索に新しいアイデアや方法も提供します。今後もさらに素晴らしい結果を期待しています!