حقق مجال النمذجة التوليدية ثلاثية الأبعاد تقدمًا ملحوظًا، باعتبارها ابتكارًا خارقًا، أحدثت تقنية GaussianCube تغييرات ثورية في النمذجة ثلاثية الأبعاد بكفاءتها العالية ودقتها العالية. إنه يتغلب على قيود طريقة NeRF التقليدية ويحقق تركيبًا عالي الدقة للأصول ثلاثية الأبعاد من خلال خوارزميات تركيب غاوسية مبتكرة مقيدة الكثافة وخوارزميات نقل مثالية، مما يقلل بشكل كبير من متطلبات المعلمات ويبسط عملية النمذجة. لدى GaussianCube مجموعة واسعة من التطبيقات، تشمل إنشاء كائنات ثلاثية الأبعاد غير مشروطة ومشروطة، وإنشاء الصور الرمزية الرقمية، وتوليف محتوى النص إلى ثلاثي الأبعاد، وقد أظهر تحسينات في الأداء تصل إلى 74% في التجارب.
لقد حقق مجال النمذجة التوليدية ثلاثية الأبعاد طفرة تقنية جديدة تسمى GaussianCube تجاوزت NeRF التقليدية (حقول الإشعاع العصبي) وأحدثت تغييرات ثورية في النمذجة ثلاثية الأبعاد.
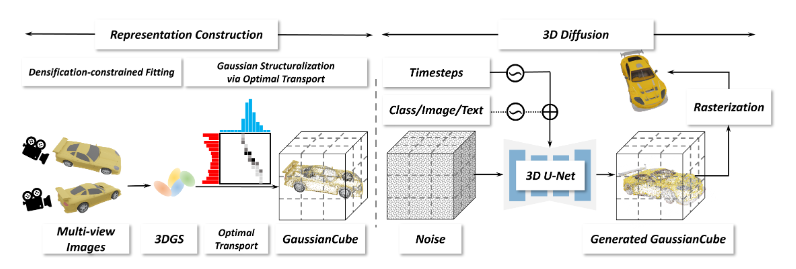
GaussianCube عبارة عن طريقة تمثيل ثلاثية الأبعاد منظمة بشكل واضح تتيح تركيبًا عالي الدقة للأصول ثلاثية الأبعاد من خلال خوارزمية تركيب Gaussian جديدة مقيدة بالكثافة، مع ضمان عدد ثابت من Gaussian المجانية المستخدمة في عملية التركيب.
مدخل المنتج: https://top.aibase.com/tool/gaussiancube
تستخدم هذه التقنية خوارزمية إرسال مثالية لإعادة ترتيب الغاوسيين في شبكة فوكسل محددة مسبقًا، مع الحفاظ على علاقة البنية المكانية للغاوسيين. يتيح ذلك للباحثين اعتماد شبكة U-Net ثلاثية الأبعاد القياسية بشكل مباشر باعتبارها الشبكة الأساسية لنمذجة الانتشار دون تصميم شبكة معقد. إن ضغط GaussianCube يقلل بشكل كبير من متطلبات المعلمات للنمذجة التوليدية ثلاثية الأبعاد. بالمقارنة مع الطرق التقليدية، يتم تقليل عدد المعلمات بشكل كبير، وبالتالي تبسيط عملية النمذجة.
أجرى الباحثون تجارب واسعة النطاق في جوانب متعددة، بما في ذلك إنشاء كائنات ثلاثية الأبعاد غير مشروطة ومشروطة، وإنشاء الصور الرمزية الرقمية، وتوليف محتوى النص إلى ثلاثي الأبعاد. النتائج التجريبية مثيرة للإعجاب. لقد حقق GaussianCube تحسينات في الأداء تصل إلى 74% في مجموعات بيانات متعددة، مما حقق نتائج رائدة في الصناعة في كل من المؤشرات الرقمية والجودة المرئية.



يتضمن إطار عمل GaussianCube مرحلتين رئيسيتين: بناء التمثيل والانتشار ثلاثي الأبعاد. في مرحلة بناء التمثيل، يتم الحصول على عدد ثابت من Gaussian ثلاثي الأبعاد من خلال خوارزمية تركيب Gaussian مقيدة الكثافة ويتم تنظيمها في GaussianCube من خلال خوارزمية نقل مثالية. في مرحلة الانتشار ثلاثي الأبعاد، يتم استخدام نموذج نشر ثلاثي الأبعاد لإنشاء GaussianCube من الضوضاء الغوسية، ويدعم مجموعة متنوعة من الإشارات الشرطية للتحكم في عملية التوليد.
هذه التكنولوجيا ليست فقط قادرة على إنتاج أصول ثلاثية الأبعاد عالية الجودة، ولكنها توفر أيضًا تأثيرات بصرية جذابة للغاية، مما يدل على إمكاناتها الكبيرة كتمثيل عالمي للجيل ثلاثي الأبعاد. يمثل تقديم GaussianCube قفزة كبيرة في تقنية النمذجة التوليدية ثلاثية الأبعاد ويوفر أداة قوية لإنشاء محتوى ثلاثي الأبعاد في المستقبل.
النقاط الأساسية:
- GaussianCube: طريقة تمثيل ثلاثية الأبعاد منظمة وواضحة جديدة.
- خوارزمية مبتكرة: تركيب غاوسي مقيد بالكثافة مع خوارزمية نقل مثالية.
- النمذجة المبسطة: لا حاجة لتصميم شبكة معقد، فقط قم بتطبيق شبكة U-Net ثلاثية الأبعاد القياسية مباشرةً.
- أداء عالي: أظهرت النتائج التجريبية تحسنًا في الأداء بنسبة تصل إلى 74%.
- تطبيقات متنوعة: إنشاء كائنات ثلاثية الأبعاد غير مشروطة ومشروطة، وإنشاء الصور الرمزية الرقمية، وتوليف النص إلى ثلاثي الأبعاد.
بشكل عام، أدى ظهور تقنية GaussianCube إلى جلب إمكانيات جديدة إلى مجال النمذجة التوليدية ثلاثية الأبعاد. مما لا شك فيه أن كفاءتها العالية ودقتها وآفاق تطبيقها الواسعة ستعزز إنشاء المحتوى ثلاثي الأبعاد إلى آفاق جديدة. هذه التكنولوجيا ليست ذات أهمية كبيرة في الأوساط الأكاديمية فحسب، بل سيكون لها أيضًا تأثير عميق في الصناعة.