smard power forecasting
1.0.0
Ce référentiel sert à prévoir la consommation électrique allemande.
Basé et inspiré de :
Source des données : SMARD
Mettez tous les fichiers téléchargés dans :
/example/dataset # there is already used dataset included if you pull, but you could update
Consultez le fichier Forecast.Rmd pour voir comment vous pouvez exécuter ce code sur une version mise à jour de SMARD-Data.
Bibliothèques utilisées :
# Probably needed
# Load Packages
# library(fhswf)
# library(tsibbledata)
# library(broom)
# library(readr)
# library(datasets)
# library(timeDate)
# library(qlcal)
# library(corrplot)
# library(mgcv)
# library(MEFM)
# library(TTR)
packages <- c(
"devtools",
"ggplot2",
"dplyr",
"tsibble",
"fable",
"fabletools",
"feasts",
"distributional",
"lubridate",
"tidyr",
"forecast",
"zoo",
"scales",
"fable.prophet"
)
install.packages(packages)
library(devtools)
library(ggplot2)
library(dplyr)
library(tsibble)
library(fable)
library(fabletools)
library(feasts)
library(distributional)
library(lubridate)
library(tidyr)
library(forecast)
library(zoo)
library(scales)
library(fable.prophet)
Essayez de travailler dans le dossier exemple/pour commencer.
# Define datapaths
power_consum_path <- "dataset\stunde_2015_2024\Realisierter_Stromverbrauch_201501010000_202407090000_Stunde.csv"
power_consum_smard_prediction_path <- "dataset\propgnose_vom_smard\Prognostizierter_Stromverbrauch_202401010000_202407090000_Stunde.csv"
# Load Smard Prediction
power_consum_smard_prediction_loaded <- load_power_consum(path=power_consum_smard_prediction_path)
raw_smard_pred <- power_consum_smard_prediction_loaded$raw_data
cleaned_smard_pred <- power_consum_smard_prediction_loaded$cleaned_data
cleaned_smard_pred <- cleaned_smard_pred |>
mutate(.model = "SMARD")
names(cleaned_smard_pred)[names(cleaned_smard_pred) == "PowerConsum"] <- ".mean"
# Load PowerConsum Data
power_consum_loaded <- load_power_consum(path=power_consum_path)
raw_power_consum <- power_consum_loaded$raw_data
cleaned_power_consum <- power_consum_loaded$cleaned_data
# Generate more features
cleaned_power_consum$localName[is.na(cleaned_power_consum$localName)] = "Working-Day"
cleaned_power_consum$MeanLastWeek <- rollapply(cleaned_power_consum$PowerConsum, width = 24*8, FUN = function(x) mean(x[1:(24*8-25)]), align = "right", fill = NA)
cleaned_power_consum$MeanLastTwoDays <- rollapply(cleaned_power_consum$PowerConsum, width = 24*3, FUN = function(x) mean(x[1:(24*3-25)]), align = "right", fill = NA)
cleaned_power_consum$MaxLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) max(x[1:(24*2-25)]), align = "right", fill = NA)
cleaned_power_consum$MinLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) min(x[1:(24*2-25)]), align = "right", fill = NA)
Les fonctionnalités suivantes ont été générées à partir de l'ensemble de données et de l'API Holiday :
| Indice | Nom de la colonne | Description |
|---|---|---|
| 1 | DateDe | Pour la validation de DateIndex (similaire, mais brut) |
| 2 | Consommation d'énergie | Consommation d'énergie en MW |
| 3 | DateIndex | Horodatage (aaaa-mm-jj hh:mm:ss) |
| 4 | Jour de la semaine | Mo, Di, Mi, Do, Fr, Sa, So (jours de la semaine en allemand) |
| 5 | Date | Date (aaaa-mm-jj) |
| 6 | Année | Année aaaa |
| 7 | Semaine | Numéro de semaine 0-53 |
| 8 | Heure | Numéro d'heure 0-24 |
| 9 | Mois | Numéro du mois 1-12 |
| 10 | nomlocal | Nom d'un jour férié pour l'horodatage |
| 11 | Jour de travail | 1/0 Si Workday (Werktag) alors 1 |
| 12 | Mo | 1/0 Si lundi alors 1 |
| 13 | Di | 1/0 Si mardi alors 1 |
| 14 | Mi | 1/0 Si mercredi alors 1 |
| 15 | Faire | 1/0 Si jeudi alors 1 |
| 16 | Fr | 1/0 Si vendredi alors 1 |
| 17 | Sa | 1/0 Si samedi alors 1 |
| 18 | Donc | 1/0 Si dimanche alors 1 (pas nécessaire si du lundi au samedi sont utilisés) |
| 19 | Vacances | 1/0 Si c'est un jour férié alors 1 |
| 20 | Jour de travailVacancesWeek-end | S'il s'agit d'un jour férié, d'un week-end ou d'un jour ouvrable (pour les parcelles, c'est Char.) |
| 21 | Jour De VacancesEtTravail | 1/0 Si le jour férié tombe un jour ouvrable, alors 1 |
| 22 | LastDayWasNotWorkDay | 1/0 Si le dernier jour n'était pas un jour ouvrable alors 1 |
| 23 | LastDayWasNotWorkDayAndNowWorkDay | 1/0 Si le dernier jour n'était pas un jour ouvrable et que c'est maintenant un jour ouvrable, alors 1 |
| 24 | NextDayIsNotWorkDayAndNowWorkDay | 1/0 Si le lendemain n'est pas un jour ouvrable et maintenant un jour ouvrable alors 1 |
| 25 | LastDayWasHolidayAndNotWeek-end | 1/0 Si le dernier jour était un jour férié et non un week-end alors 1 |
| 26 | NextDayIsHolidayAndNotWeek-end | 1/0 Si le lendemain est un jour férié et non un week-end alors 1 |
| 27 | Nom de vacances | similaire à localName (Nom du séjour) |
| 28 | FinDeL'Année | 1/0 Si c'est la fin de l'année (Semaine 52 ou 53) |
| 29 | PremièreSemaineDeL'Année | 1/0 Si c'est le début de l'année (Semaine 1) |
| 30 | VacancesProlongées | 1/0 Jours fériés décalés (6 heures le jour suivant) |
| 31 | VacancesLissé | HolidayExtend + sin(2*pi(Heure)+1)/24) |
| 32 | MoyenneSemaineDernière | Consommation d'énergie moyenne de la semaine dernière (Shift : 24*8-25) |
| 33 | MoyenneDerniersDeuxJours | Consommation électrique moyenne des deux derniers jours (Shift : 24*3-25) |
| 34 | MaxLastOneDay | Consommation d'énergie maximale du dernier jour (Shift : 24*2-25) |
| 35 | MinDernierUnJour | Consommation d'énergie minimale du dernier jour (Shift : 24*2-25) |
Dans cette étude, il existe un ensemble de données sur la consommation d'énergie en Allemagne du SMARD pour les années 2015 à 2024.
La figure 1 montre l'ensemble de données brutes avec les valeurs manquantes (rouge), les horodatages dupliqués (rouge foncé) et la consommation d'énergie au fil du temps (gris), résolution horaire. Avec une valeur manquante et un doublon chaque année, il était facile de nettoyer l'ensemble de données. Dans l'ensemble, un ensemble presque propre. Après avoir nettoyé l'ensemble de données, il existe des observations plausibles concernant la consommation électrique :
Il existe une approche simple pour combler les lacunes en prenant la dernière observation (possible, car la résolution est suffisamment grande et car il ne manque que peu de valeurs). La première valeur a été conservée pour les doublons.
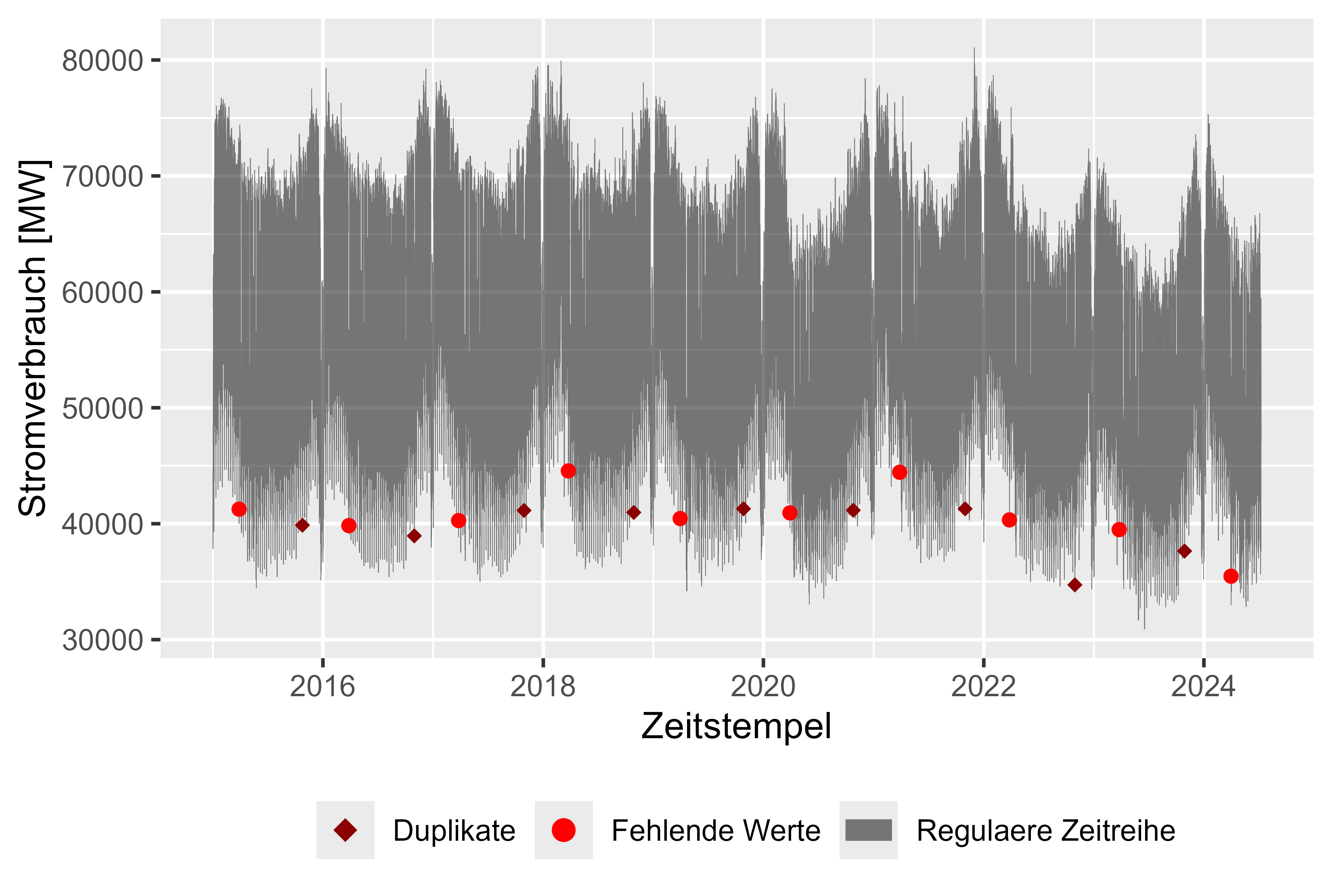Figure 1 Consommation d'énergie brute
local_name_colors <- c(
"Christi Himmelfahrt" = palette()[2],
"Erster Weihnachtstag" = palette()[2],
"Karfreitag" = palette()[2],
"Neujahr" = palette()[2],
"Ostermontag" = palette()[2],
"Pfingstmontag" = palette()[2],
"Reformationstag" = palette()[2],
"Tag der Arbeit" = palette()[2],
"Tag der Deutschen Einheit" = palette()[2],
"Zweiter Weihnachtstag" = palette()[2],
"Regulärer Tag" = palette()[1]
)
week_colors <- c(
"Mo" = palette()[1],
"Di" = palette()[1],
"Mi" = palette()[1],
"Do" = palette()[1],
"Fr" = palette()[1],
"Sa" = palette()[2],
"So" = palette()[2]
)
working_colors <- c("1" = "#2E9FDF", "0" = "#FC4E07")
whw_colors <- c(
"FeiertagnKein Wochenende" = "black",
"Kein FeiertagnKein Wochenende" = "red",
"Kein FeiertagnWochenende" = "orange",
"FeiertagnWochenende" = "blue"
)
p <- cleaned_power_consum |>
gg_tsdisplay(PowerConsum, plot_type = "partial", lag = 100)
ggsave(
"plots/power_consum_acf_pacf.png",
plot = p,
width = 5.5,
height = 3.7,
dpi = 600
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MinLastOneDay.png",
x = "MinLastOneDay",
y = "PowerConsum",
x_label = "Minimaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MaxLastOneDay.png",
x = "MaxLastOneDay",
y = "PowerConsum",
x_label = "Maximaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastWeek.png",
x = "MeanLastWeek",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 7 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastTwoDays.png",
x = "MeanLastTwoDays",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 2 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkdayHolidayWeekend",
file_name = "plots\workday_holiday_weekend_histogram.png",
colors = whw_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "Holiday",
file_name = "plots\holiday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Werktag oder Wochenende",
name_1 = "Feiertag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "HolidayAndWorkDay",
file_name = "plots\holiday_workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Werktag",
name_1 = "Feiertag am Werktag"
)
plot_by_group(
cleaned_power_consum,
group_name = "HolidayName",
file_name = "plots\holiday_boxplot.png",
colors = local_name_colors,
title = "Übersicht der einzelnen Feiertage",
y="PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "Weekday",
file_name = "plots\weekday_boxplot.png",
colors = week_colors,
title = "Übersicht der einzelnen Wochentage",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_boxplot.png",
colors = working_colors,
title = "Übersicht, ob Feiertag (FALSE) oder Werktag (TRUE)",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_column(
df = cleaned_power_consum,
x = "Hour",
y = "PowerConsum",
x_label = "Stunden",
y_label = "Stromverbrauch [MW]",
file_name = "plots\hour_boxplot.png",
title = "Übersicht der einzelnen Stunden"
)
plot_by_column(
df = cleaned_power_consum,
x = "Month",
y = "PowerConsum",
x_label = "Monate",
y_label = "Stromverbrauch [MW]",
file_name = "plots\month_boxplot.png",
title = "Übersicht der einzelnen Monate"
)
plot_by_column(
df = cleaned_power_consum,
x = "Week",
y = "PowerConsum",
x_label = "Woche",
y_label = "Stromverbrauch [MW]",
file_name = "plots\week_boxplot.png",
title = "Übersicht der einzelnen Wochen"
)
plot_by_column(
df = cleaned_power_consum,
x = "Year",
y = "PowerConsum",
x_label = "Jahr",
y_label = "Stromverbrauch [MW]",
file_name = "plots\year_boxplot.png",
title = "Übersicht der einzelnen Jahre"
)
plot_year_month_week_day(
df=cleaned_power_consum,
date_column="DateIndex",
y="PowerConsum",
from_year=2015,
to_year=2024,
from_week=0,
to_week=53,
year_for_week=2018,
from_day=1,
to_day=30,
month_for_day=4,
year_for_day=2018,
from_month=1,
to_month=12,
year_for_month=2018,
holiday="Holiday",
day_of_week = "Weekday"
)
Les sections suivantes approfondiront de plus en plus les données. Nous commencerons ici par la représentation annuelle.
La figure 2 est une représentation annuelle des années 2015-2024. Nous pouvons remarquer ici qu'au début de l'année il y a une augmentation de la consommation d'énergie et qu'en fin d'année il y a une diminution (Noël, Nouvel An). Dans l'ensemble, cela ressemble à une forme de sourire ou à un arc.
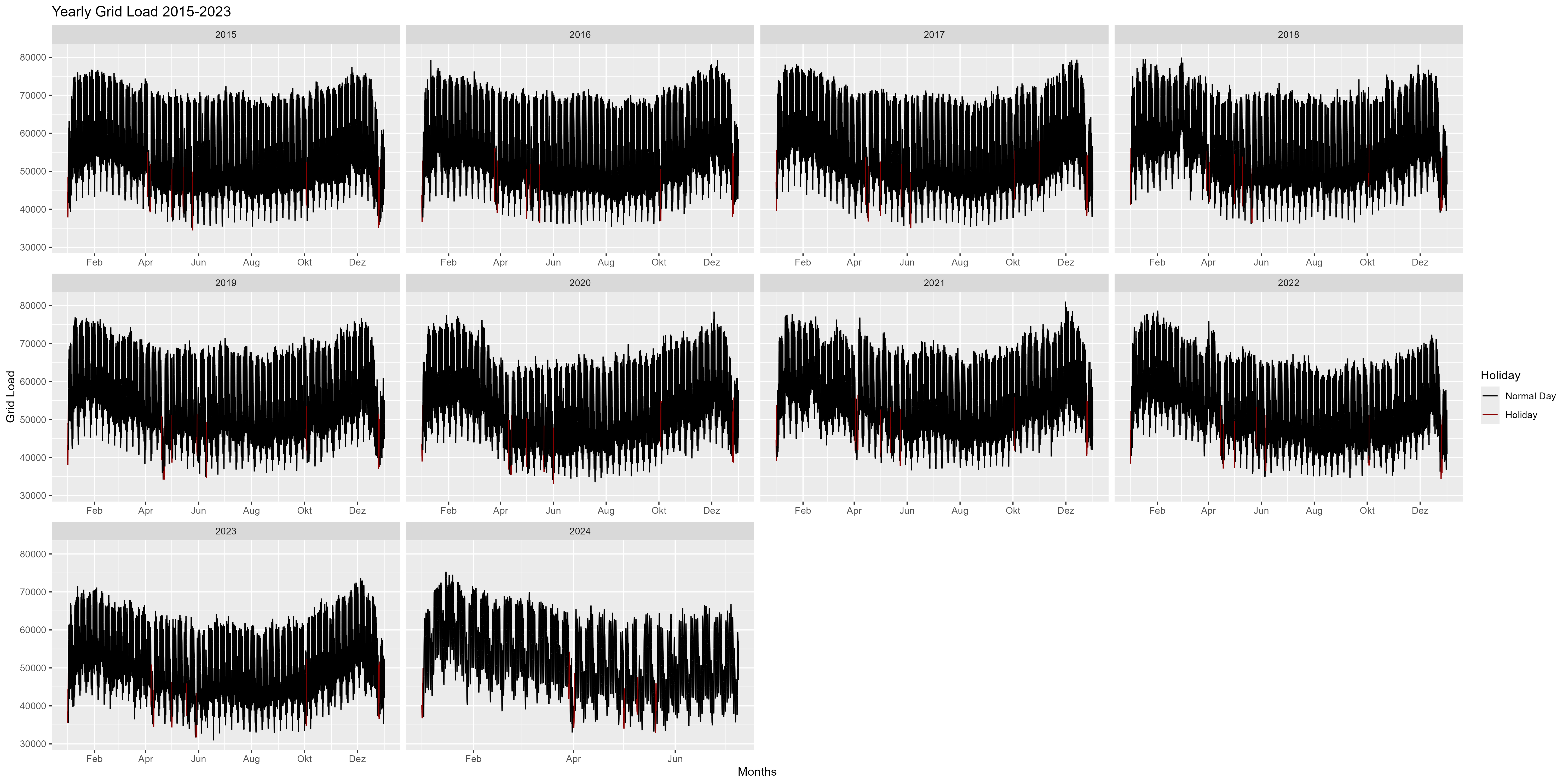Figure 2 Consommation d'énergie, chaque année, sous forme d'une seule facette
Essayons de regrouper toutes les années et de les diviser en semaines. Les boxplots de la figure 3 combinent toutes les années. Nous pouvons voir le motif plus en détail. Le début et la fin d'une année sont représentés en rouge et montrent une diminution par rapport à la « forme de sourire » habituelle.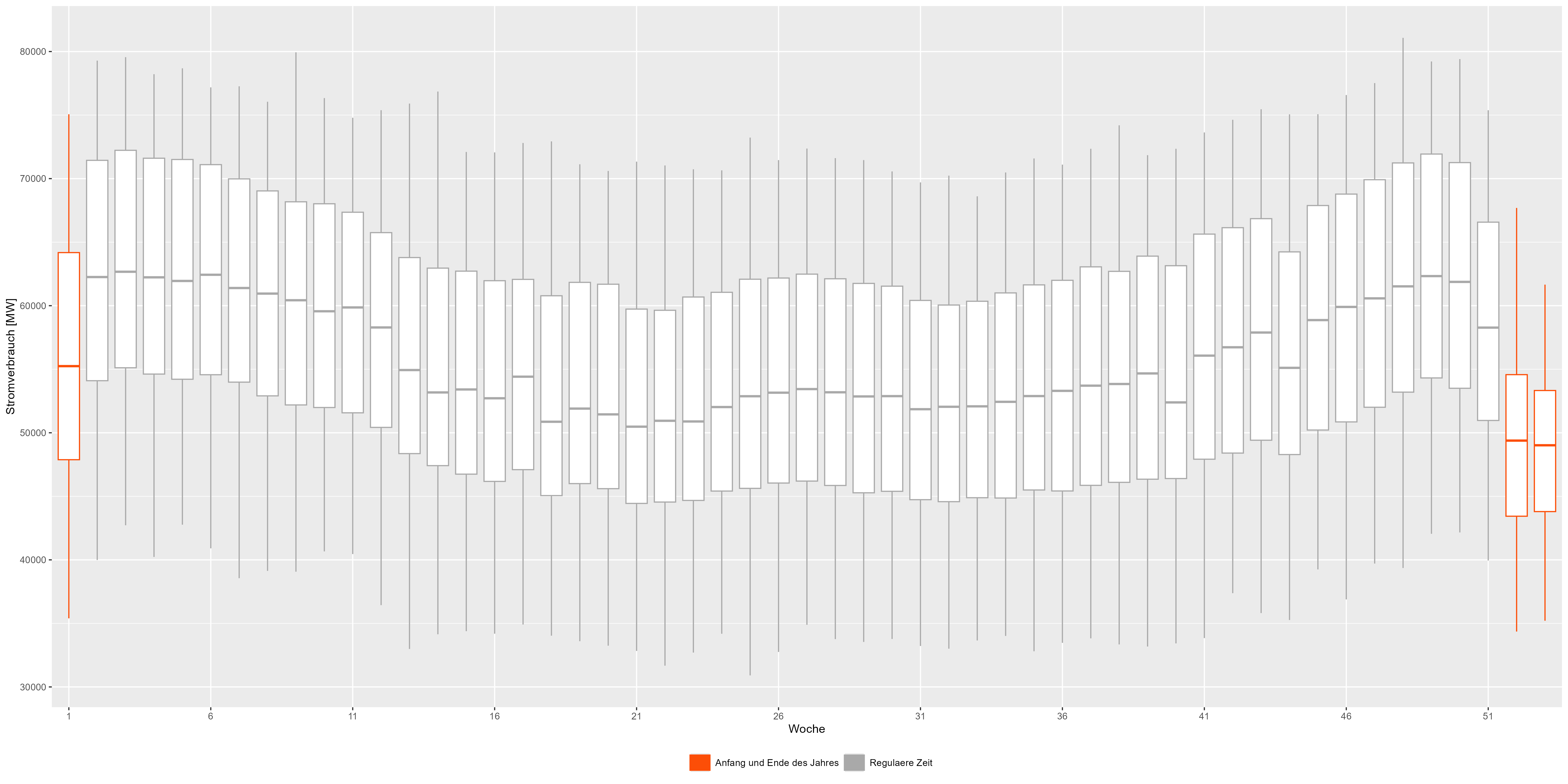
Figure 3 Données agrégées hebdomadaires sur la consommation d'énergie
Allons plus en détail et regardons l'année 2018 par exemple. La figure 4 est la représentation mensuelle de l'année 2018. Ici on peut observer plus en détail la fin de l'année. Vers le 24 décembre, on constate une diminution de la consommation électrique. A noter également ici les week-ends et les jours fériés (rouge). Une baisse pour tous les week-ends et pour tous les jours fériés.
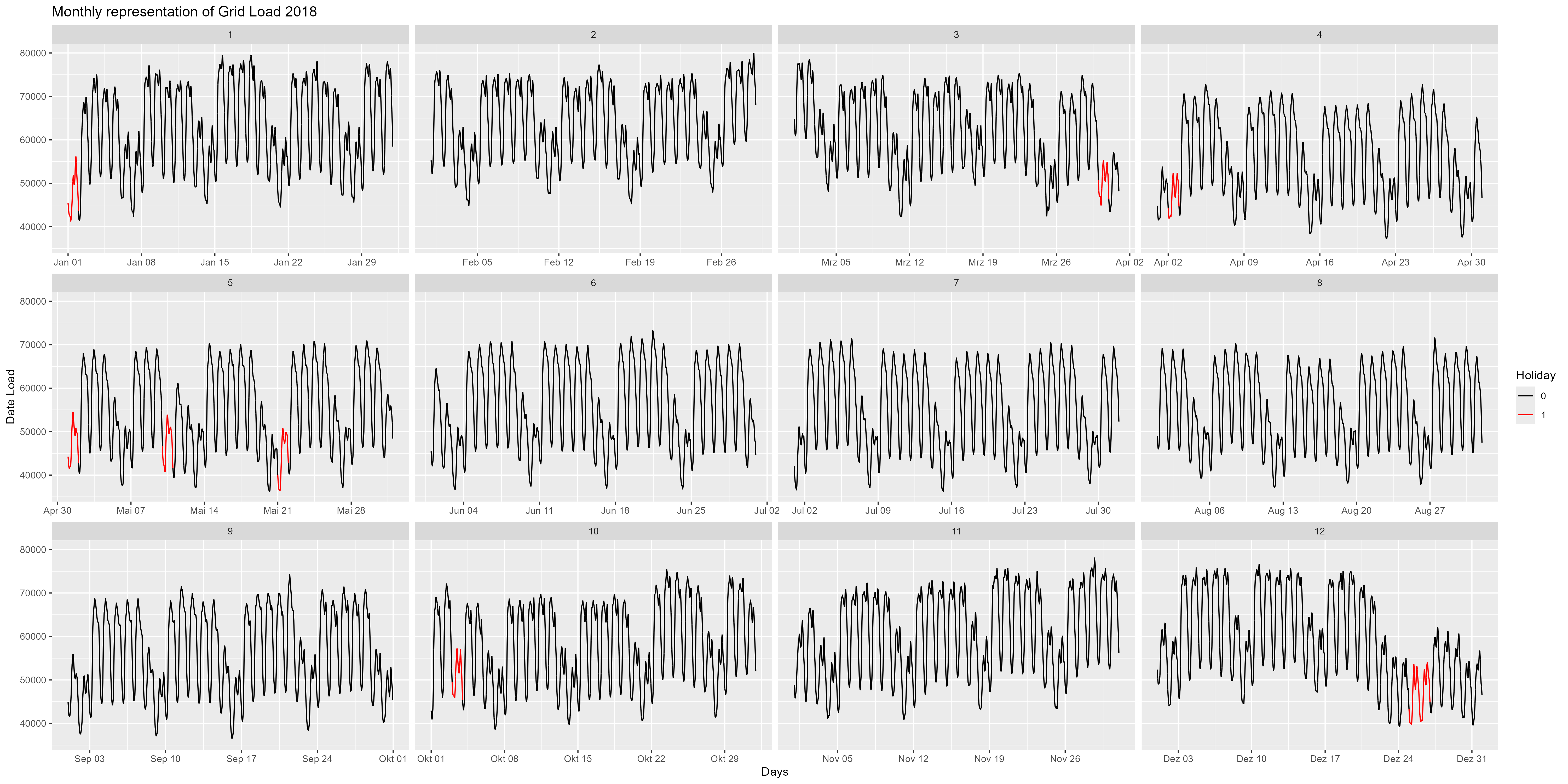Figure 4 Consommation d'énergie, chaque mois sous forme d'une seule facette
On pourrait aller encore plus loin et vérifier la représentation horaire des données. La figure 5 montre le boxplot agrégé pour chaque heure. Il y a également une diminution de la nuit (21h00-06h00) et une augmentation de la journée/du temps de travail (06h00-21h00). Également un motif qui doit être inclus dans le modèle.
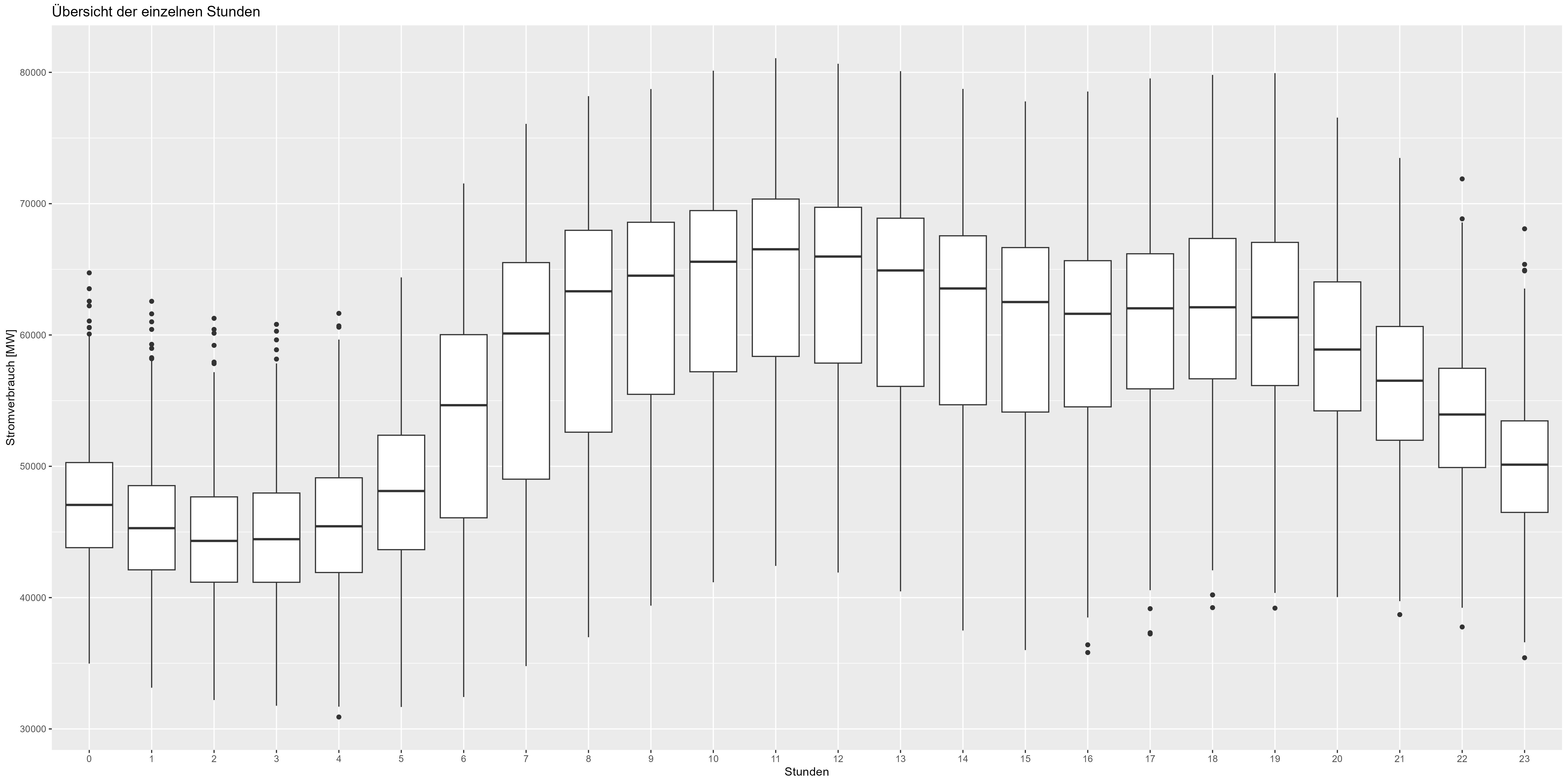Figure 5 Données agrégées horaires de consommation d’énergie
Parlons des jours de la semaine. Comme prévu, la consommation d'énergie du week-end diminue. "Durchschnitt" est la moyenne. La figure 6 montre tous les jours de la semaine (agrégés) au fil des ans. Il y a une diminution de ~10 000 MW pour les week-ends.
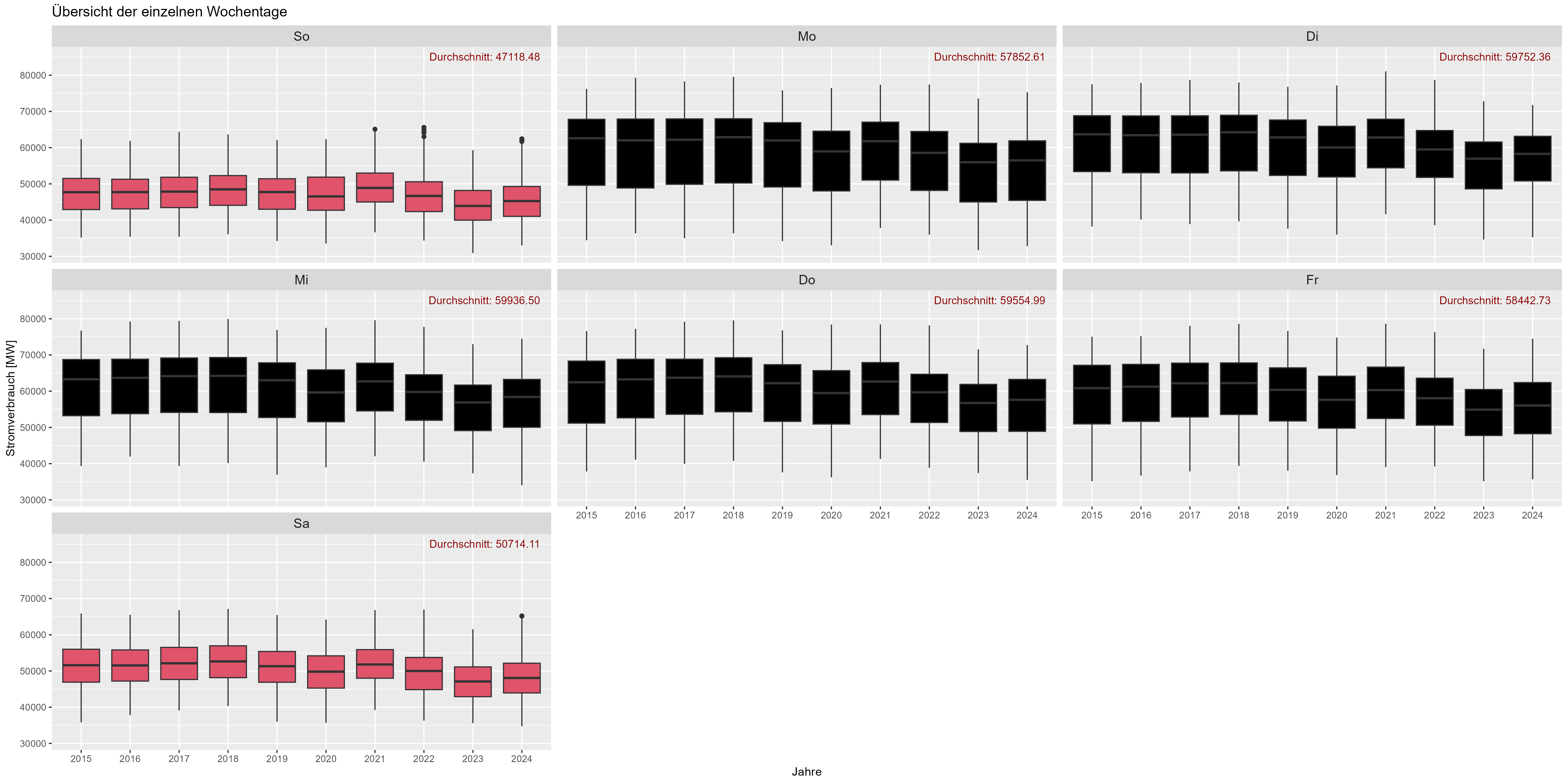Figure 6 Consommation d'énergie "effet jour de la semaine"
La figure 8 montre l'effet vacances. "Durchschnitt" est la consommation moyenne d'énergie au fil des années. Il y a une augmentation significative de la consommation d'énergie pendant les « jours ouvrables » (gris foncé) par rapport aux jours fériés (rouge). Nous pourrions supposer ici que les vacances agissent comme des week-ends pour la consommation d'énergie".
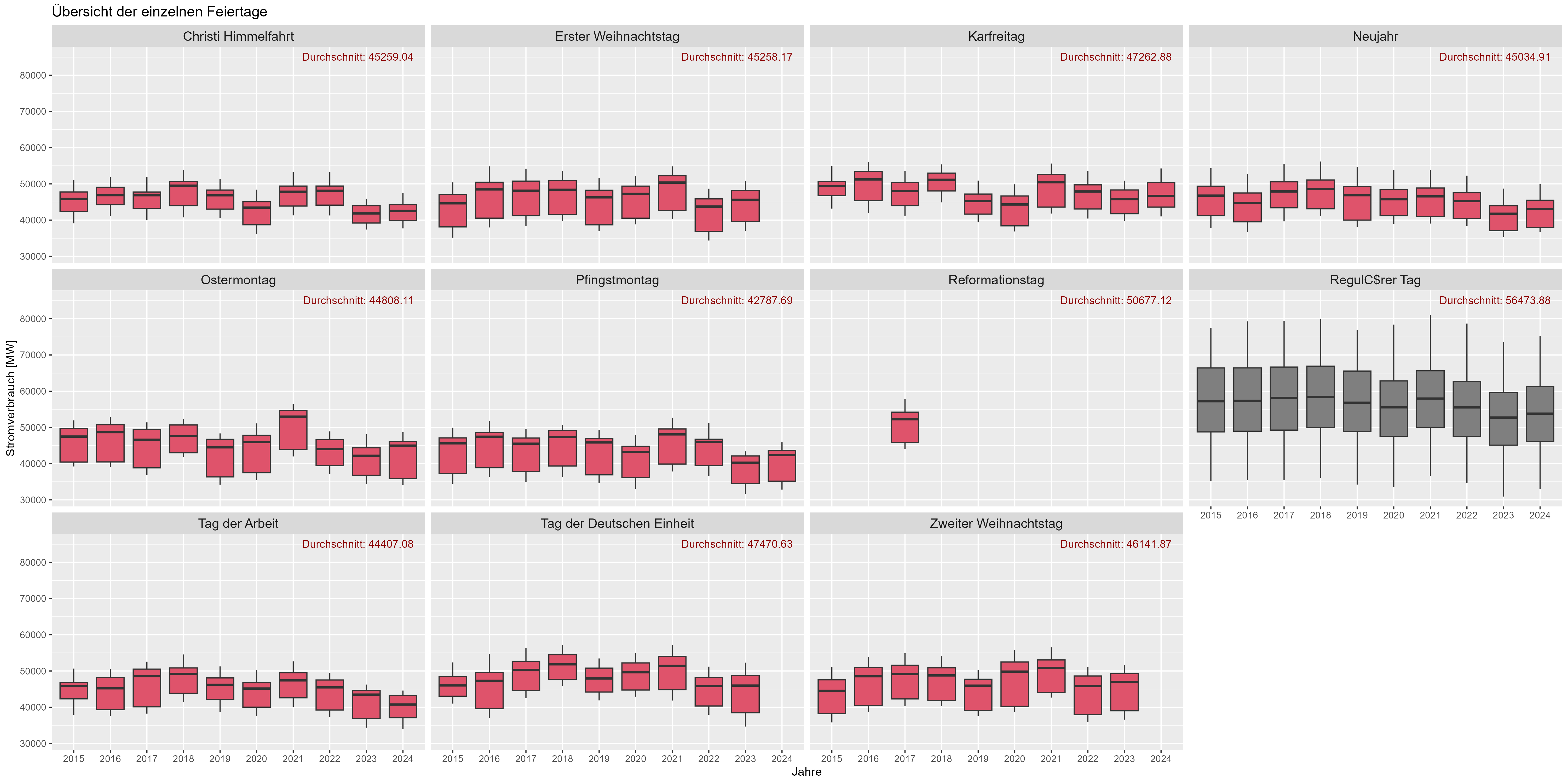Figure 6 Consommation d'énergie "effet vacances"
La figure 7 représente différents comportements pour différents jours. Il existe 4 catégories. "Feiertag Kein Wochenende" signifie que c'est un jour férié, mais pas un week-end. "Feiertag Wochenende" signifie que c'est un jour férié et un week-end. "Kein Feiertag Kein Wochenende" signifie que c'est un jour de travail normal et "Kein Feiertag Wochenende" signifie que c'est juste le week-end. Nous pouvons observer des distributions similaires pour les jours de travail non réguliers, comme supposé.
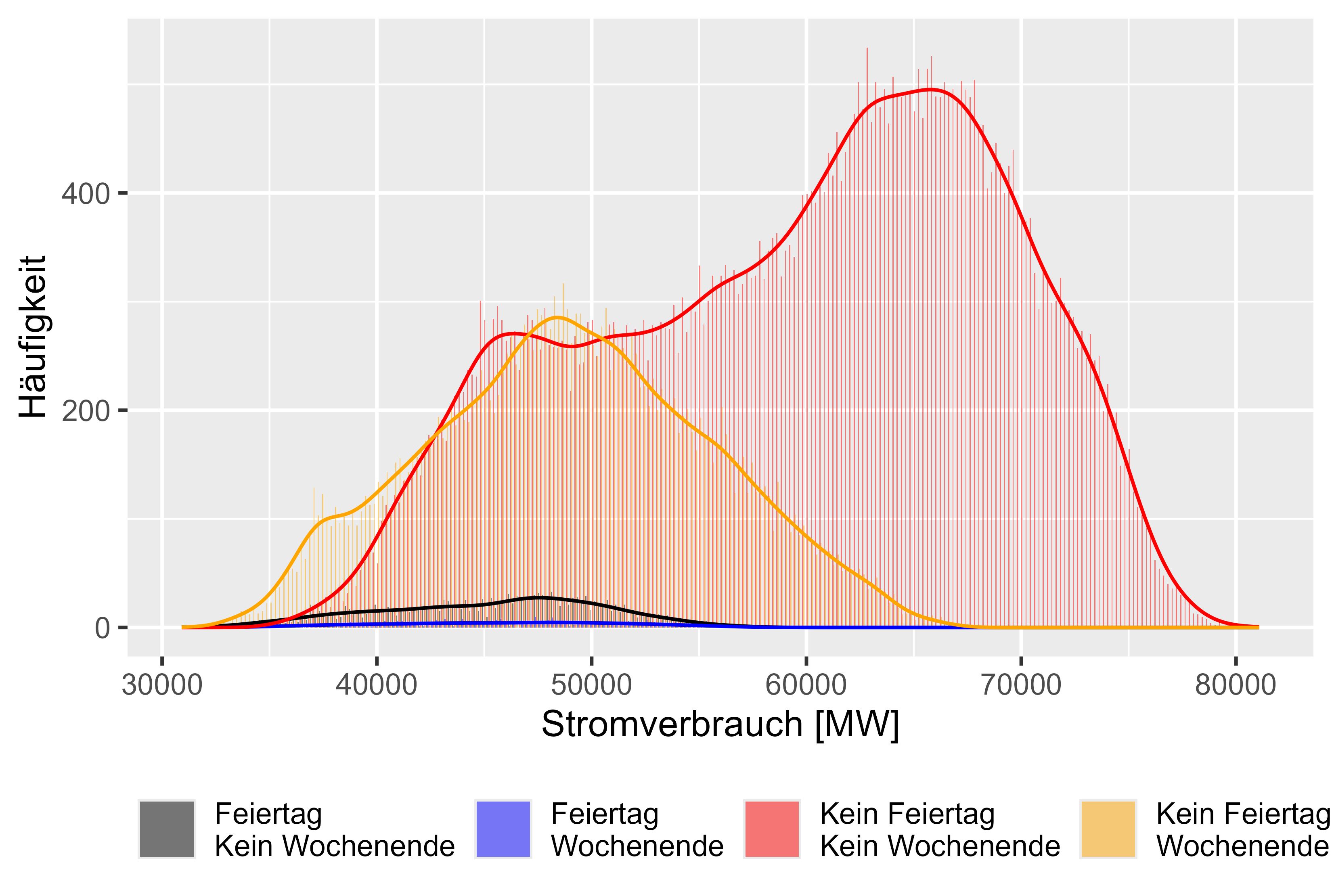Figure 7 Comparaison de la consommation électrique « différents effets »
Les valeurs décalées telles que MeanLastTwoDays, MeanLastWeek, MaxLastOneDay et MinLastOneDay sont des fonctionnalités générées.
Similaire à celui discuté dans DOI : 10.1109/TPWRS.2011.2162082 - Prévision de charge à court terme basée sur un modèle additif semi-paramétrique
Les figures 8 à 11 (les rouges représentent les jours non ouvrables) représentent ces valeurs décalées par rapport à la consommation électrique réelle.
Il existe une légère corrélation pour ces fonctionnalités générées.
# Check Correlation
cor <- cor(cleaned_power_consum[sapply(cleaned_power_consum, is.numeric)], method = c("pearson", "kendall", "spearman"), use = "complete.obs")
| Fonctionnalité | Corrélation avec PowerConsum |
|---|---|
| VacancesLissé | -0,556194 |
| MoyenneSemaineDernière | 0,389044 |
| MoyenneDerniersDeuxJours | 0,201253 |
| MaxLastOneDay | 0,320193 |
| MinDernierUnJour | 0,348583 |
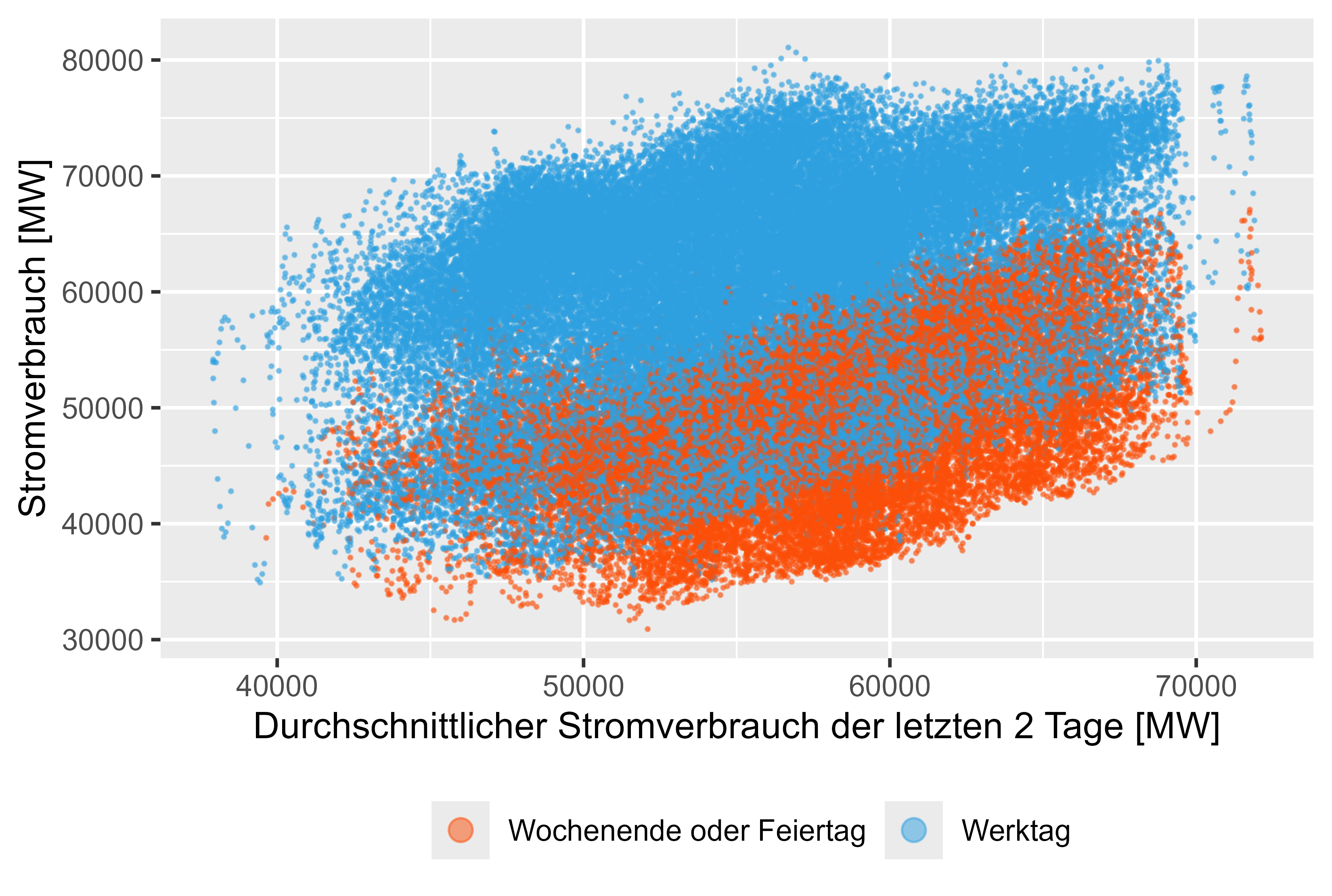Figure 8 Consommation d'énergie - MeanLastTwoDays
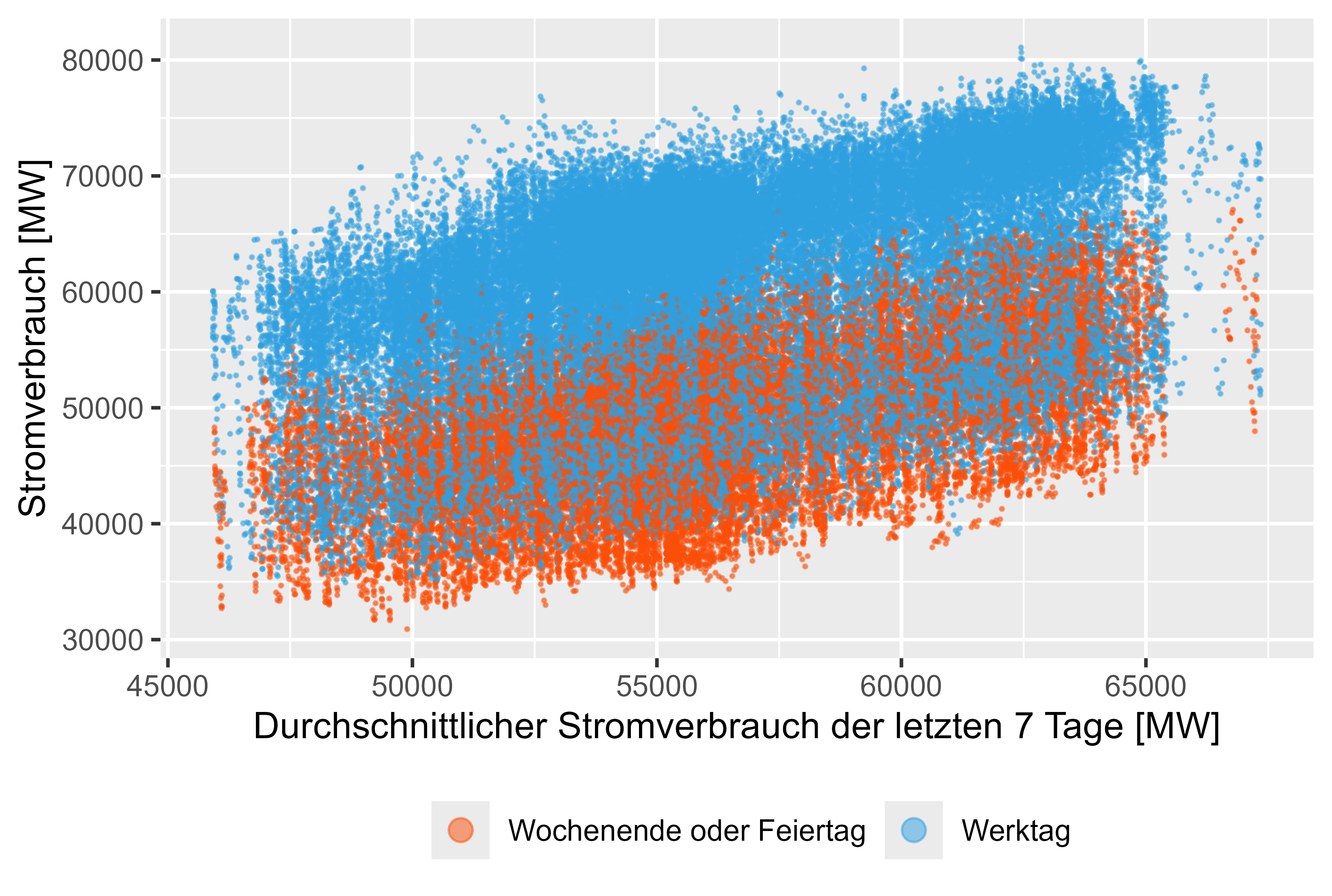Figure 9 Consommation d'énergie - MeanLastWeek
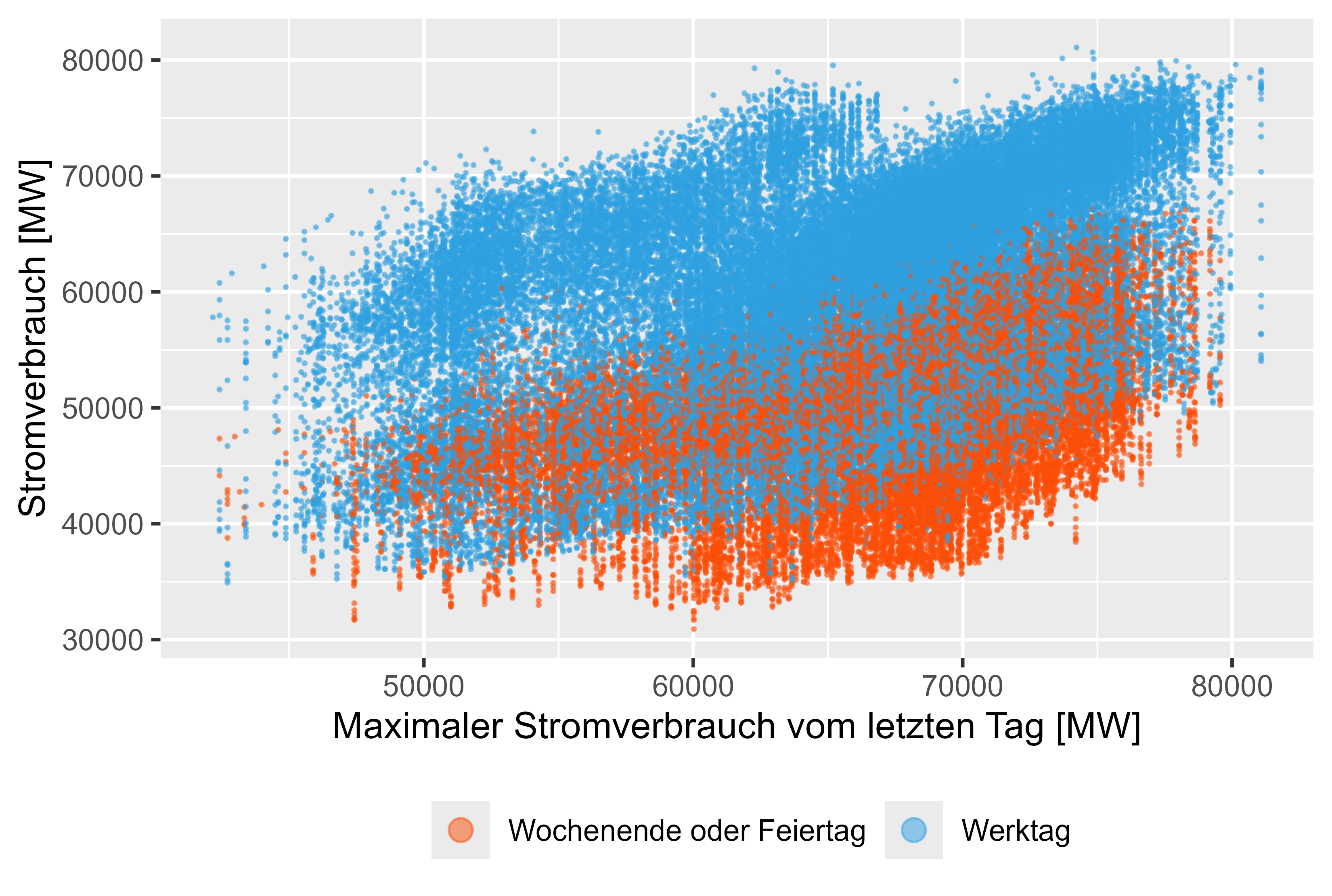Figure 10 Consommation d'énergie - MaxLastOneDay
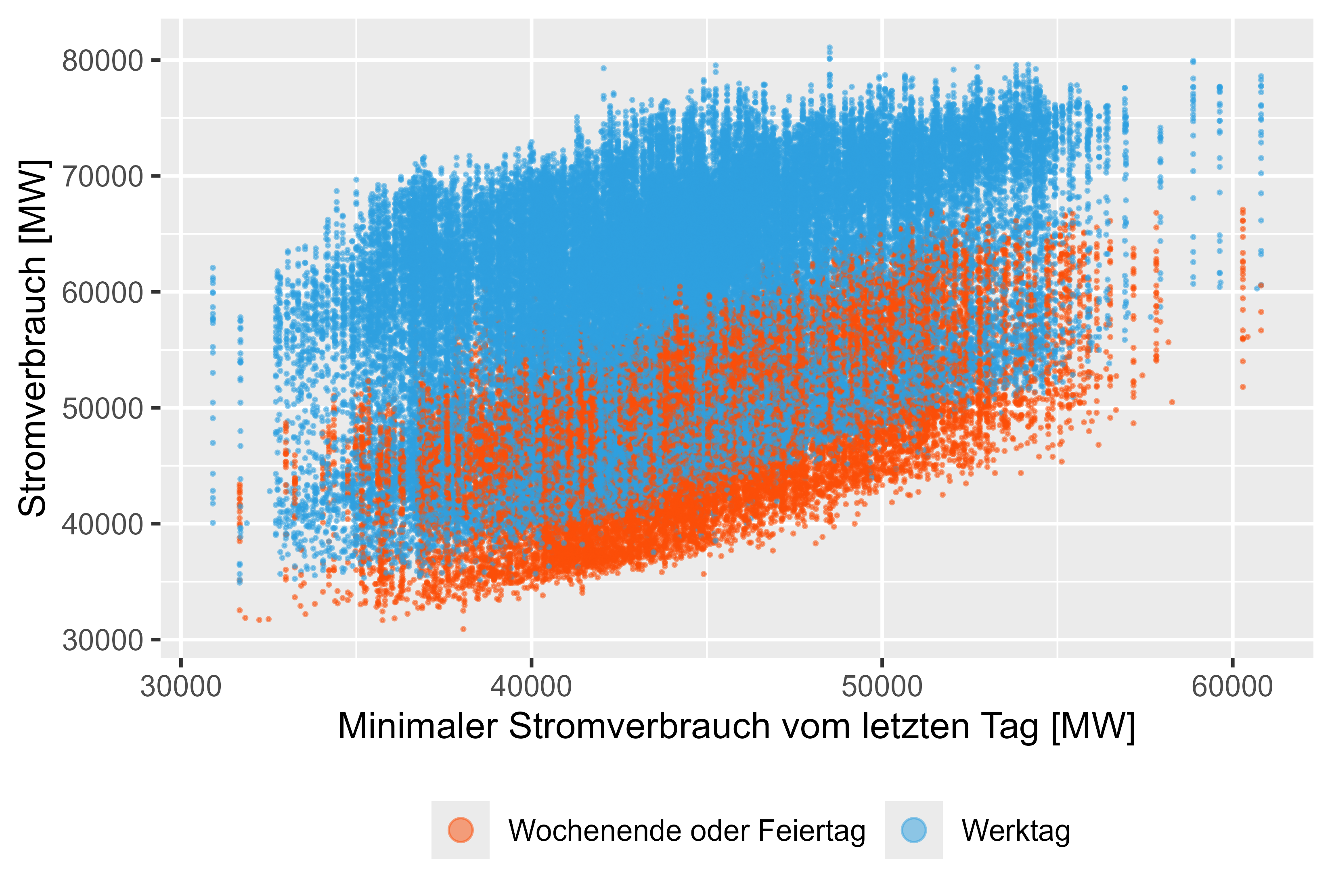Figure 11 Consommation d'énergie - MinLastOneDay
Il existe une saisonnalité complexe. Pour la résolution horaire, il existe une saisonnalité annuelle, hebdomadaire et quotidienne. Ce qui doit être suivi par le modèle. La solution ici est celle discutée dans Prévisions : principes et pratiques, chapitre 12.1 Saisonnalité complexe pour utiliser des termes de Fourier pour représenter et assembler via cos() et sin() la saisonnalité complexe.
Nous pouvons jeter un petit coup d'œil sur les tracés ACF et PACF, il y a peu de pics significatifs, mais ce n'est que la représentation de 96 valeurs décalées. Si nous prenons environ 9 000 observations décalées sur un an, nous obtiendrons une saisonnalité complexe. C'est pourquoi il est plus facile d'utiliser le terme de Fourier. Cela n'a pas non plus bien fonctionné en trouvant simplement les composants PDQ et pdq en
ARIMA(...
stepwise=FALSE,
greedy=FALSE,
approx=FALSE)
lui-même. De plus, le temps de formation augmente considérablement sans les termes de Fourier.
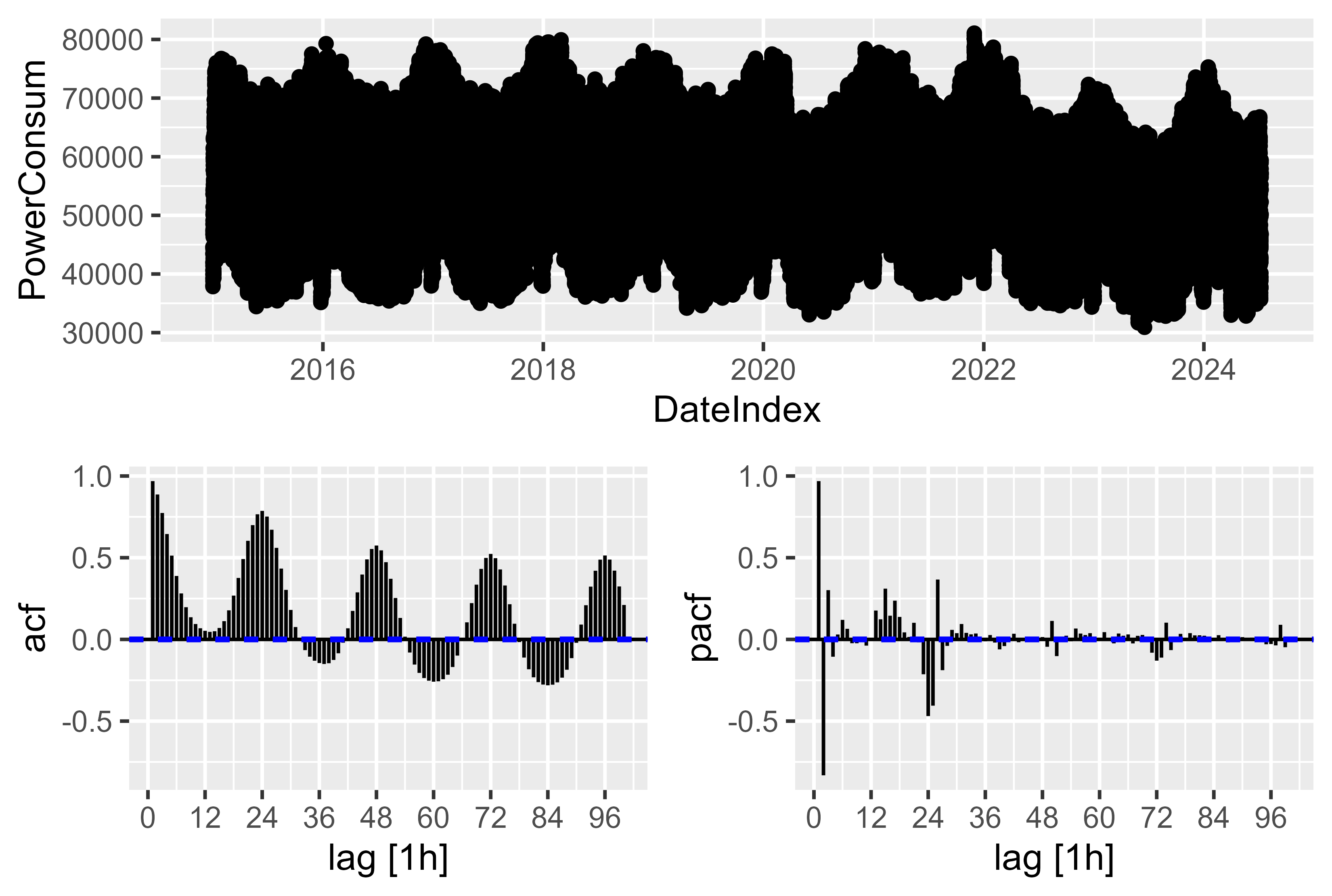Figure 12 Consommation d'énergie - ACF PACF Tracé de la consommation d'énergie brute
Les meilleures combinaisons de fonctionnalités trouvées dans ce travail sont :
Pour comparer les modèles, nous utilisons les métriques MAE et MAPE. SMARD est le modèle de la "Bundesnetzagentur" de la page SMARD. Le modèle Prophet a également été testé, il a été performant, mais pas assez bon.
Les valeurs prévues du SMARD ont atteint un MAPE de 3,6%. <- PAS DANS CETTE ÉTUDE.
Données de formation :
Le meilleur modèle trouvé jusqu'à présent est la guerre LHM + DHR (modèle harmonique linéaire + régression harmonique dynamique)
L'idée est d'assembler un modèle linéaire avec le modèle ARIMA. Parce qu'il était difficile pour le modèle ARIMA de gérer les variables fictives pour les vacances. Le modèle ensemble a donc aidé.
train_power_consum <- cleaned_power_consum |>
filter(year(DateIndex) > 2020 & (year(DateIndex) < 2024))
generate_models(model_name = "model/mean_naive_drift",
train_power_consum = train_power_consum)
train_power_consum_v5 <- train_power_consum |>
mutate(HolidaySmoothed = Holiday + sin(2 * pi * (as.numeric(Hour)+1) / 24))
holiday_effect_model <- lm(
PowerConsum ~
HolidaySmoothed,
data = train_power_consum_v5
)
saveRDS(holiday_effect_model, file = "ensemble_model/version_5/holiday_effect_2021_2023.rds")
train_power_consum_v5$Residuals <- residuals(holiday_effect_model)
fit <- train_power_consum_v5 |>
model(
ARIMA = ARIMA(Residuals ~
PDQ(0,0,0)
+ pdq(d=0)
+ MeanLastWeek
+ WorkDay
+ EndOfTheYear # new
+ FirstWeekOfTheYear # new
+ MeanLastTwoDays
+ MaxLastOneDay
+ MinLastOneDay
+ fourier(period = "day", K = 6)
+ fourier(period = "week", K = 7)
+ fourier(period = "year", K = 3)
)
)
saveRDS(fit, file = "ensemble_model/version_5/arima_2021_2023.rds")
Nous pourrions visualiser l'effet et le fonctionnement du modèle. La figure 13 montre l'idée derrière ce modèle. Tout d’abord, nous ajustons le modèle LHM et calculons les résidus. Entraînez le modèle DHR par les résidus et résumez les deux. C'est un peu un miroir sur le LHM et repousse les valeurs vers le haut.
Pour le modèle LHM, nous utilisons ici une approche simple : une courbe sinusoïdale qui se répète toutes les 24 heures et diminue ou augmente les jours fériés ou ouvrables.
En prévoyant le LHM sur de nouvelles données, nous pouvons prévoir les résidus des nouvelles données. Résidus + LHM ramènent les valeurs à la position "correcte".
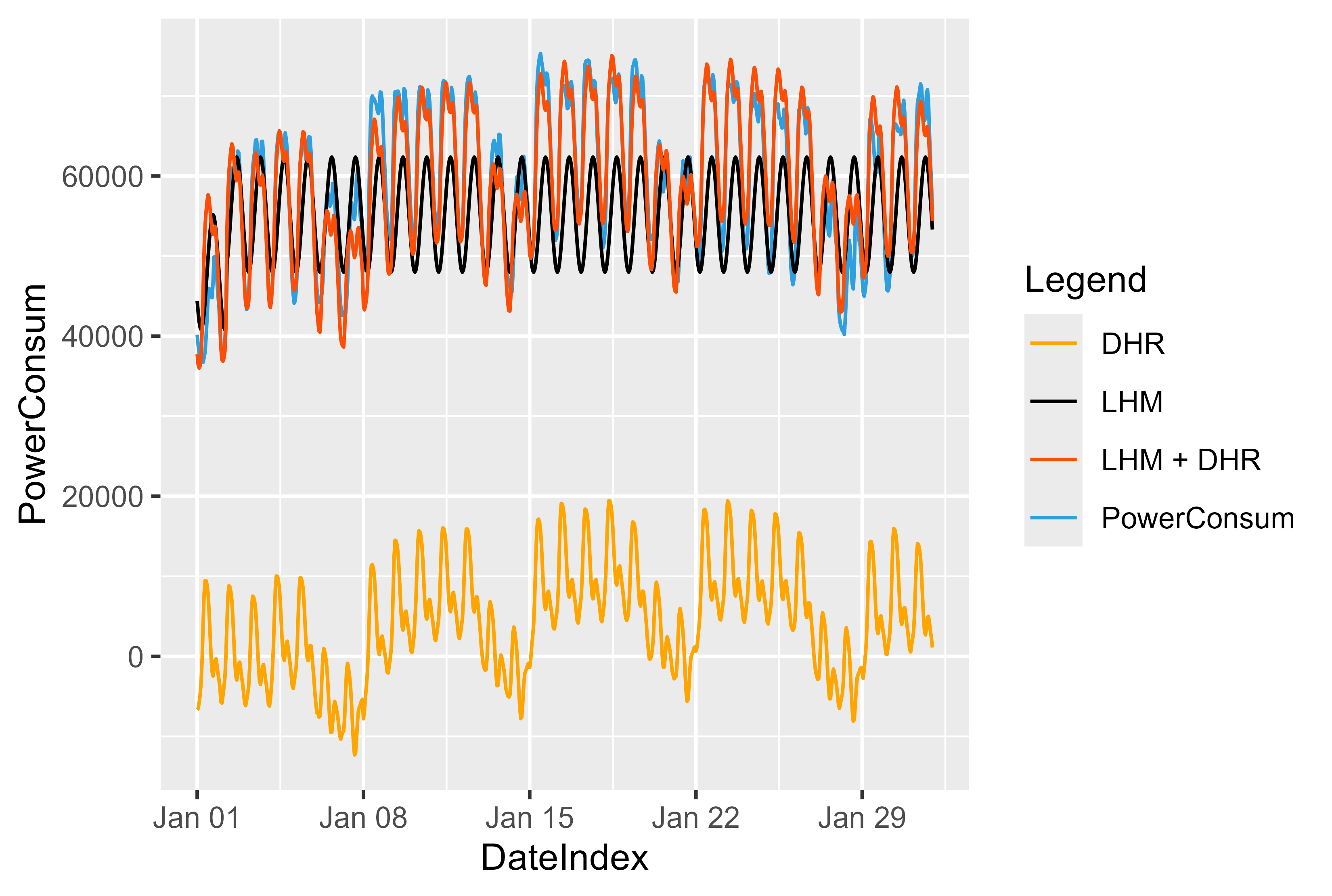Figure 13 Représentation du modèle LHM + DHR
ensembled_fc <- load_ensembled_models(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
real_data = cleaned_power_consum,
smard_fc = cleaned_smard_pred,
model_path = "ensemble_model"
)
all_forecasts_ensembled <- ensembled_fc$all_forecasts
raw_fc_ensembled <- ensembled_fc$raw_forecasts
fc <- load_all_model_results(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
smard_fc = cleaned_smard_pred,
real_data = cleaned_power_consum
)
all_forecasts <- fc$combined_forecasts
raw_fc <- fc$raw_forecasts
metric_results <- calculate_metrics(fc_data = all_forecasts, fc_data_ensembled=all_forecasts_ensembled)
# Plot best Model for single Models
name_of_best_model_for_single_model <- plot_forecast(
all_forecasts = all_forecasts,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
raw_fc = raw_fc,
month_to_plot = 1,
days_to_plot = 40
)
# Plot best Model for ensembled Models
name_of_best_model_ensembled <- plot_forecast_ensembled(
all_forecasts = all_forecasts_ensembled,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
month_to_plot = 1,
days_to_plot = 40
)
# Residuals Compared with SMARD
plot_compare_with_smard(
all_forecasts = all_forecasts_ensembled,
name_of_best_model = name_of_best_model_ensembled
)
# LHM DHM representation
plot_representation_of_lhm_dhm_components(path_dhm = "ensemble_model/version_5/arima_2021_2023.rds",
path_lhm = "ensemble_model/version_5/holiday_effect_2021_2023.rds",
from_month = 1,
to_month = 1,
raw_fc_ensembled = raw_fc_ensembled)
Un solide score de MAPE 3,8% pour la version_5 (Modèle LHM + DHR).
Examinons de plus près si nous utilisions uniquement le modèle ARIMA (arima_14). La figure 14 représente les résultats de ce modèle. Nous pouvons voir les jours fériés (orange), le week-end (rouge) et le jour normal (bleu). Il existe des valeurs aberrantes importantes pour les vacances, même s'il existait une variable fictive pour le modèle ARIMA, celle-ci n'a pas pu capturer correctement les vacances.
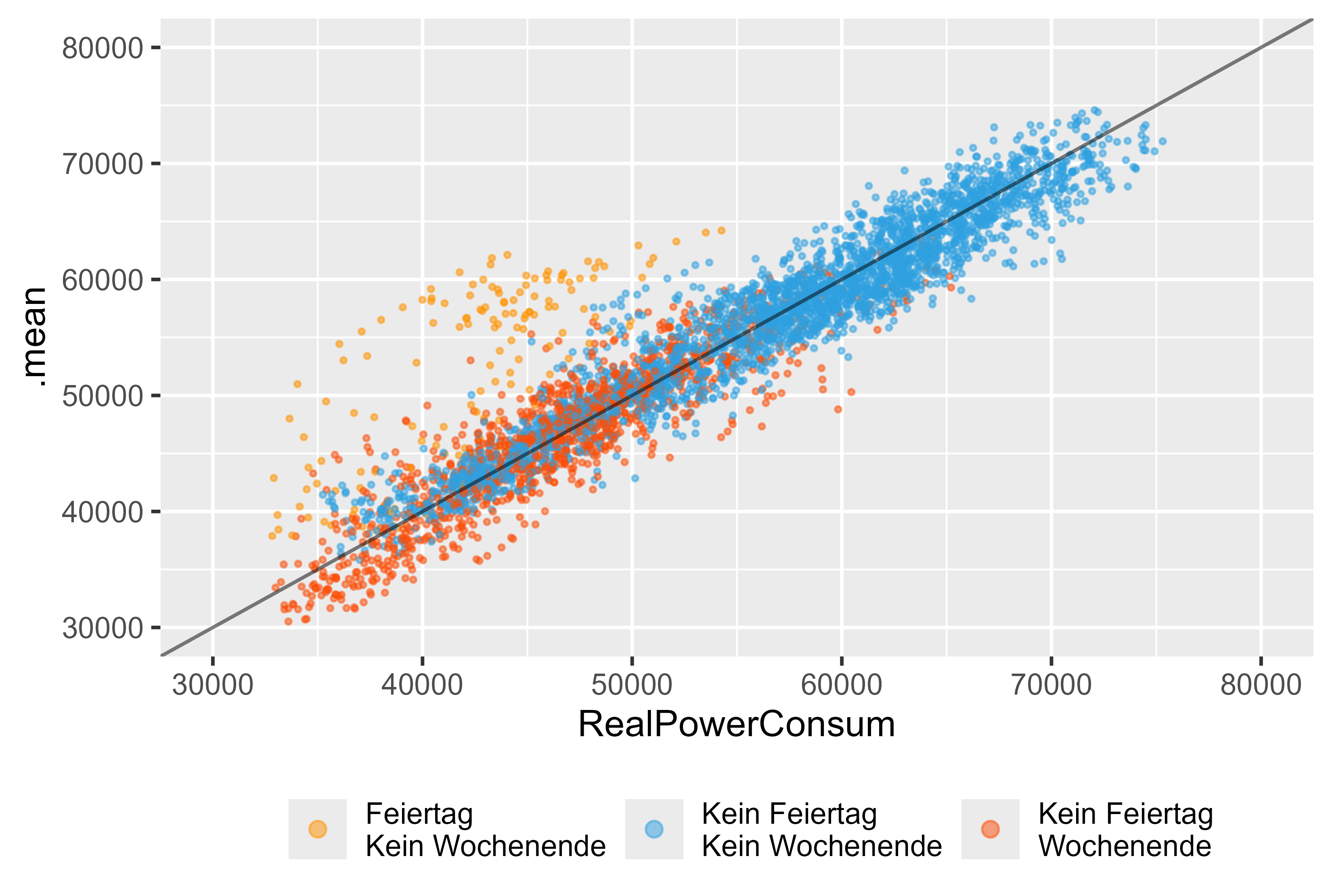Figure 14 Valeurs prévues par rapport aux valeurs réelles ARIMA (DHR, arima_14), en tant que modèle unique
En revanche le Modèle LHM + DHR présente de meilleures performances pour les vacances. La figure 15 le représente.
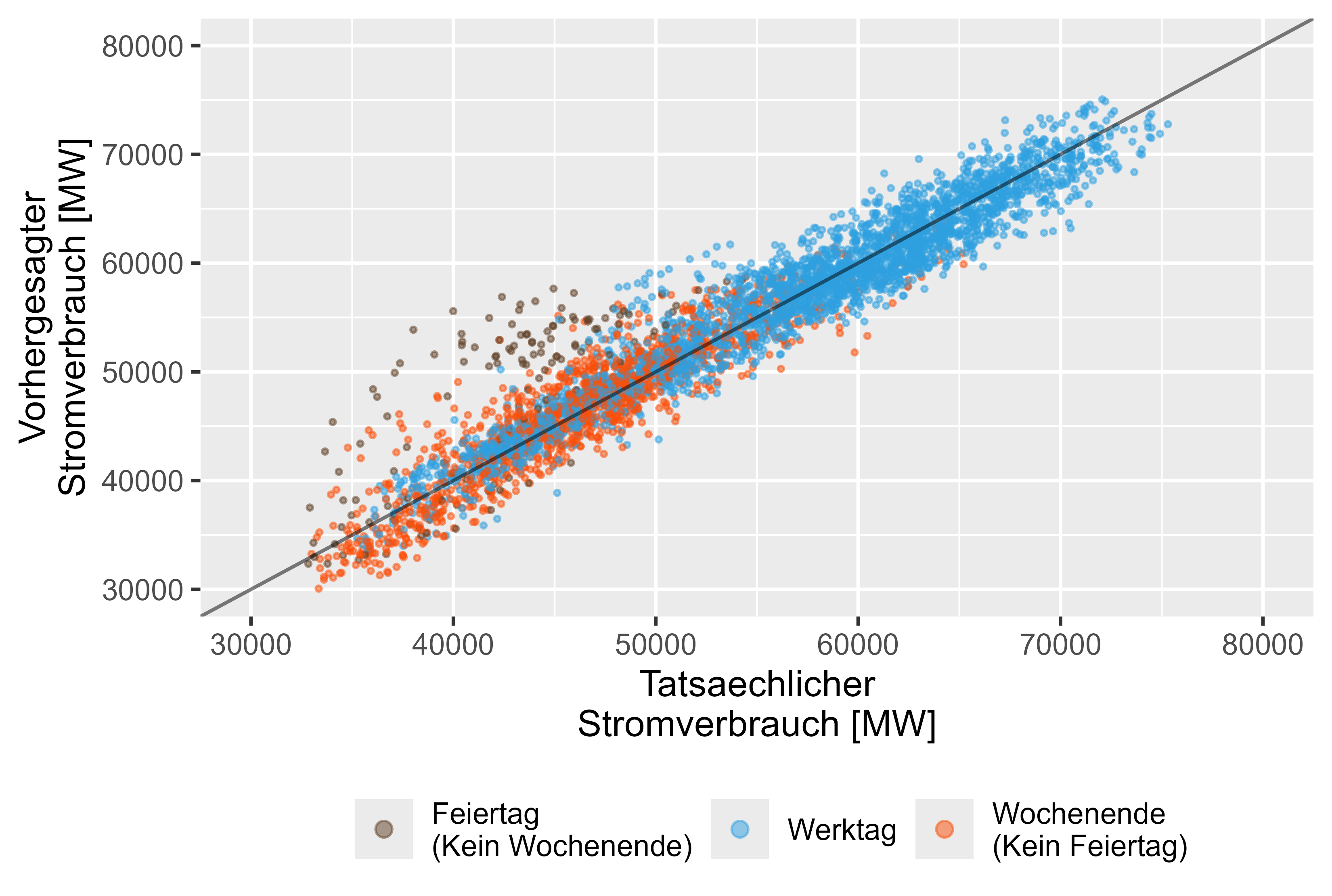Figure 15 Valeurs prévues par rapport aux valeurs réelles LHM + DHR, modèle ensemble
La figure 16 montre les prévisions pour janvier 2024. Elles semblent raisonnables.
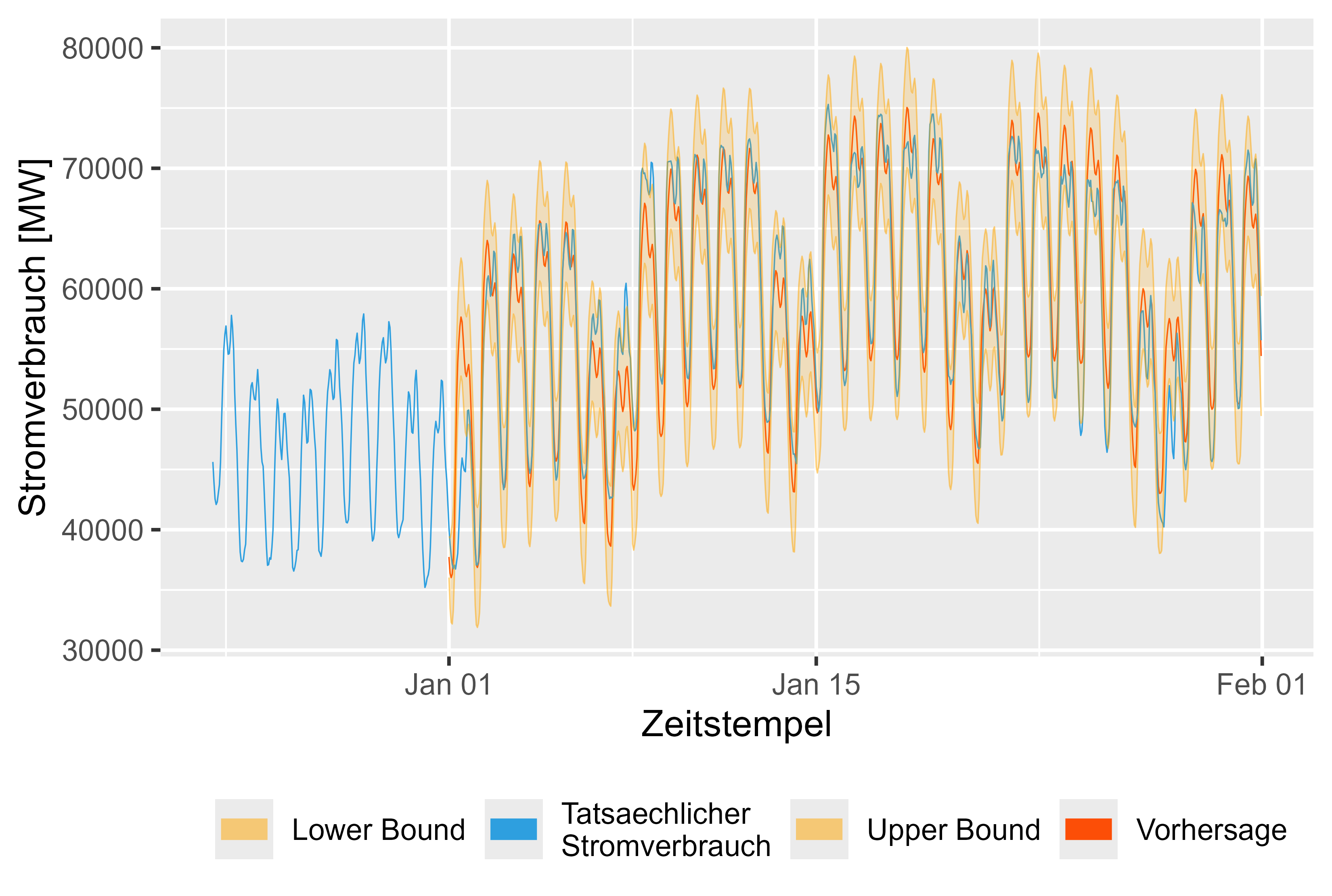Figure 16 Prévisions par rapport aux valeurs réelles LHM + DHR pour janvier 2024
De plus, les résidus du modèle par rapport au modèle SMARD semblent corrects. Il existe peu de pics qui pourraient être significatifs et qui pourraient être mieux préparés par la modélisation. Mais dans l’ensemble, c’est un bon résultat.
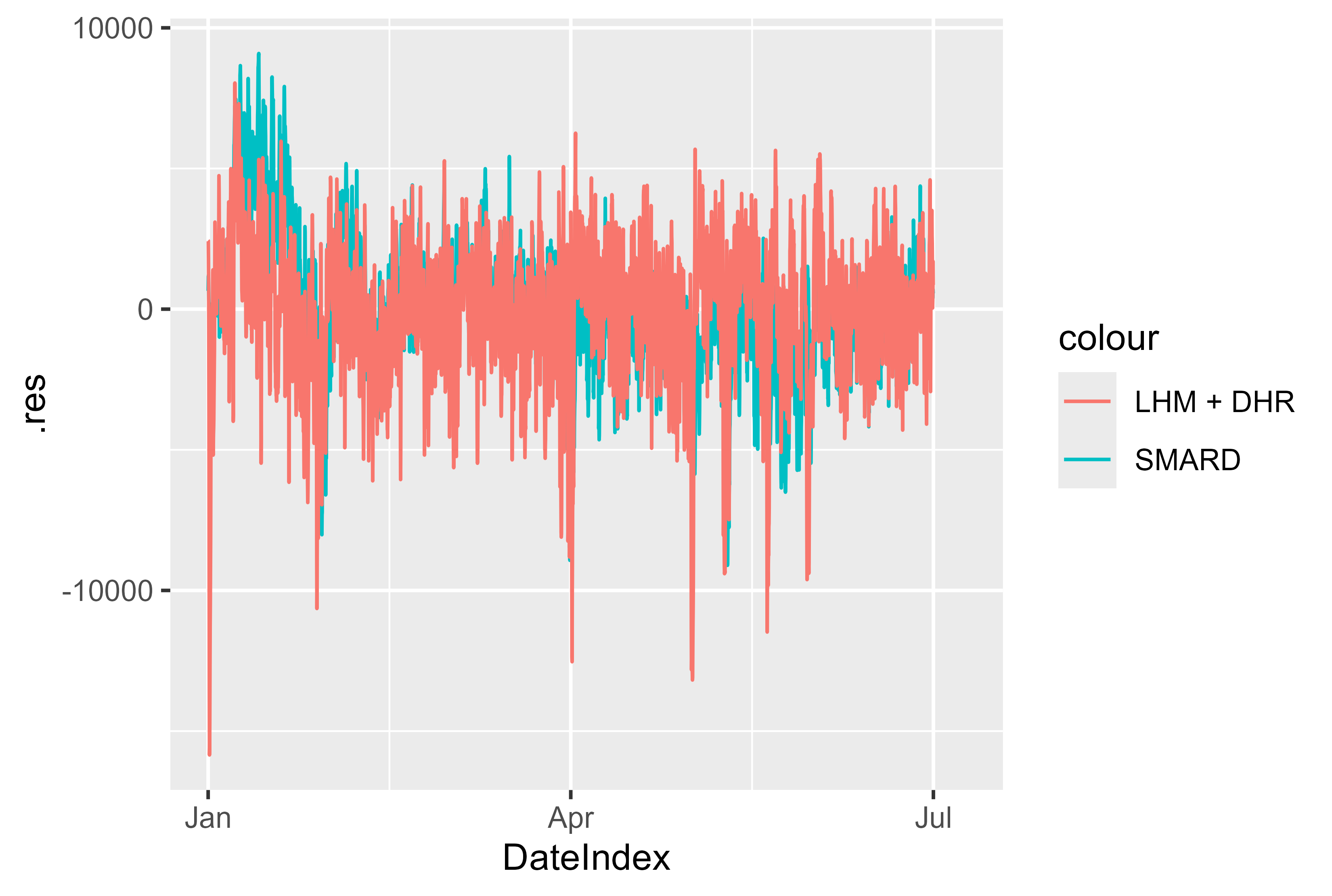Figure 17 Résidus LHM + DHR pour janvier - juillet 2024
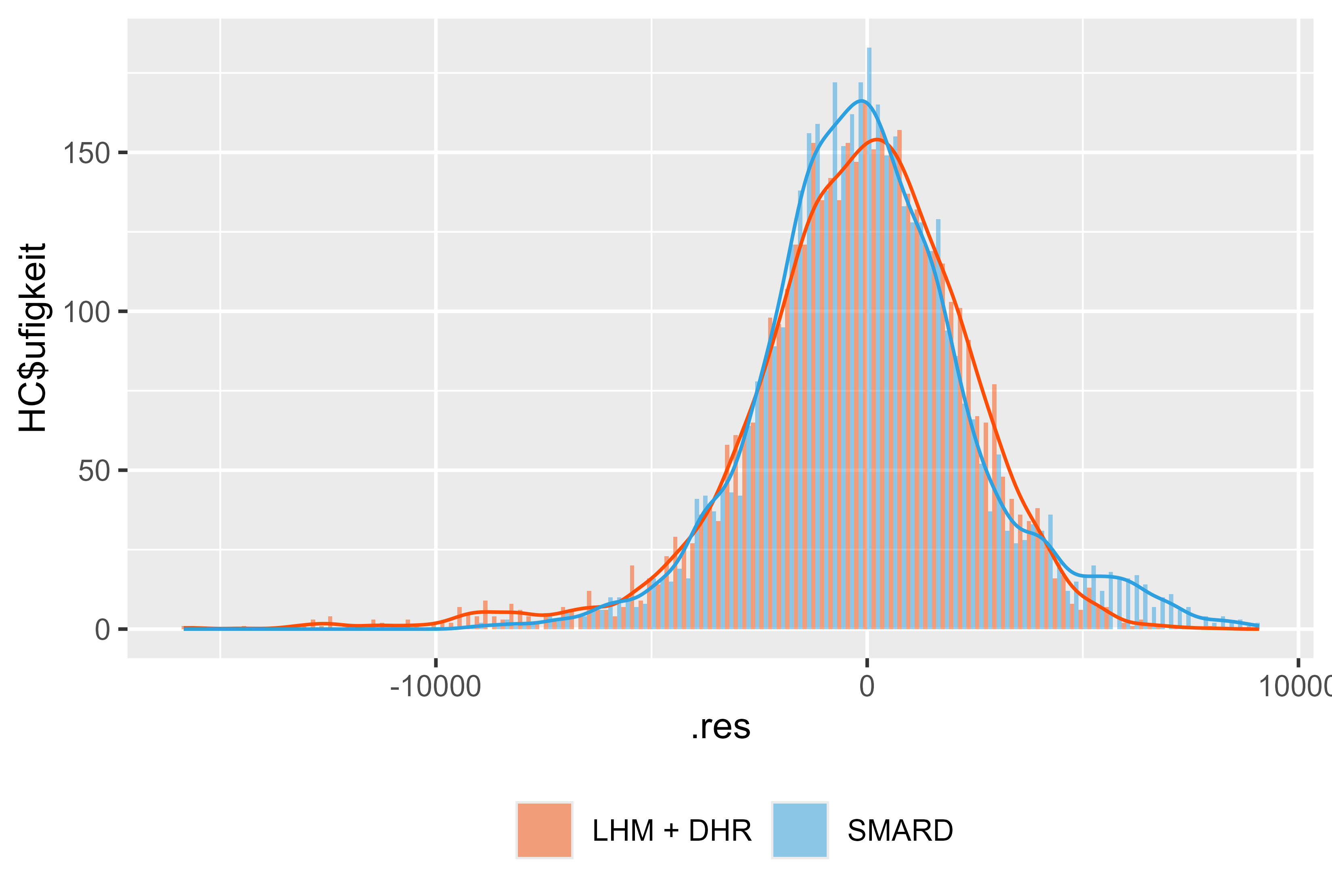Figure 18 Résidus LHM + DHR pour janvier - juillet 2024
| Indice | Nom du modèle | RMSE | MAPE | MAE | Ensemble |
|---|---|---|---|---|---|
| 2 | Observations réelles | 0,000 | 0,000000 | 0,000 | VRAI |
| 3 | SMART | 2480.693 | 3.602140 | 1869.466 | FAUX |
| 4 | SMART | 2480.693 | 3.602140 | 1869.466 | VRAI |
| 5 | version_5 | 2626.807 | 3.816012 | 1937.670 | VRAI |
| 6 | version_0 | 2613.258 | 3.846888 | 1946.314 | VRAI |
| 7 | version_7 | 2770.359 | 4.107272 | 2076.045 | VRAI |
| 8 | version_8 | 2775.441 | 4.146788 | 2091.153 | VRAI |
| 9 | version_9 | 2887.179 | 4.177841 | 2100.381 | VRAI |
| 10 | version_6 | 2906.242 | 4.216517 | 2142.092 | VRAI |
| 11 | arima_14_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FAUX |
| 12 | arima_18_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FAUX |
| 13 | version_4 | 2875.929 | 4.535388 | 2255.645 | VRAI |
| 14 | version_2 | 2905.990 | 4.580770 | 2279.624 | VRAI |
| 15 | arima_9_2021_2023.rds | 3267.160 | 4.611857 | 2302.918 | FAUX |
| 16 | arima_2_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FAUX |
| 17 | arima_4_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FAUX |
| 18 | arima_5_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FAUX |
| 19 | arima_13_2021_2023.rds | 3283.745 | 4.619636 | 2307.415 | FAUX |
| 20 | arima_10_2021_2023.rds | 3265.913 | 4.625508 | 2314.395 | FAUX |
| 21 | arima_0_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FAUX |
| 22 | arima_17_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FAUX |
| 23 | arima_16_2021_2023.rds | 3298.902 | 4.673116 | 2334.857 | FAUX |
| 24 | arima_1_2021_2023.rds | 3312.429 | 4.696342 | 2340.193 | FAUX |
| 24 | prophète_0_2021_2023.rds | 3044.849 | 4.711527 | 2435.572 | FAUX |
| 25 | arima_8_2021_2023.rds | 3332.217 | 4.716612 | 2358.085 | FAUX |
| 26 | arima_11_2021_2023.rds | 3358.020 | 4.758970 | 2388.791 | FAUX |
| 27 | arima_12_2021_2023.rds | 3430.191 | 5.022772 | 2495.067 | FAUX |
| 28 | arima_7_2021_2023.rds | 3475.671 | 5.049287 | 2510.903 | FAUX |
| 29 | version_3 | 3546.729 | 5.064654 | 2570.530 | VRAI |
| 30 | arima_15_2021_2023.rds | 3734.584 | 5.165147 | 2606.661 | FAUX |
| 31 | arima_6_2021_2023.rds | 3748.583 | 5.375326 | 2723.837 | FAUX |
| 32 | version_1 | 4495.568 | 6.483477 | 3229.647 | VRAI |
| 33 | arima_3_2021_2023.rds | 4558.982 | 6.953247 | 3453.387 | FAUX |
| 34 | tslm_0_2021_2023.rds | 6760.994 | 11.189119 | 5694.949 | FAUX |
| 35 | mean_2021_2023.rds | 9489.303 | 16.406032 | 8101.476 | FAUX |
| 36 | naive_2021_2023.rds | 14699.338 | 20.797370 | 12130.587 | FAUX |
| 37 | dérive_2021_2023.rds | 14763.692 | 20.917883 | 12200.002 | FAUX |
NOTE:
Vérifiez example/ensemble_model_2022_forecast ou example/ensemble_model_2023_forecast
Nous pourrions inclure plus de facteurs tels que :
