Otoño-2019-ITCS-8114-Algods
Este repositorio contiene los proyectos y asignaciones del curso "ITCS 6114/8114: algoritmos y estructuras de datos" . Este curso se ha tomado en el semestre de otoño de 2019, como parte de mi doctorado en UNC Charlotte.
Lista de proyectos
- Proyecto 1: Algoritmos de clasificación basados en comparación
- Proyecto 2: Algoritmos gráficos (ruta más corta de la fuente de solteros y árbol de expansión mínimo)
- Proyecto 3: Algoritmos de coincidencia de patrones
A continuación encontrará la descripción y los requisitos de los proyectos. Para obtener los detalles, vaya al directorio del proyecto correspondiente.
Proyecto 1: Algoritmos de clasificación basados en comparación
Implemente los siguientes algoritmos de clasificación y compárelos. Puede usar cualquier lenguaje de programación (por ejemplo, C/C ++, Java, Python, C#). En este proyecto, puede trabajar solo o como equipo de dos.
- Clasificación de inserción
- Fusionar
- Heapsort [basado en vector e inserte un elemento a la vez]
- Quicksort in-Place (cualquier elemento aleatorio o el primero o el último elemento de su entrada puede ser pivote).
- Quicksort modificado
- Use mediana de tres como pivote.
- Para un pequeño subproblema del tamaño <= 10, use el tipo de inserción.
Instrucciones de ejecución:
- Ejecute estos algoritmos para diferentes tamaños de entrada (por ejemplo, N = 1000, 2000, 4000, 5000, 10000 .. 40000, 50000). Generará al azar números para su matriz de entrada. Registre el tiempo de ejecución (debe tomar el promedio como se discute en la clase) y trazarlos todos en un solo gráfico contra el tamaño de la entrada. Tenga en cuenta que comparará estos algoritmos de clasificación para el mismo conjunto de datos.
- También observe y presente el rendimiento de los siguientes dos casos especiales:
- La matriz de entrada ya está ordenada.
- La matriz de entrada se clasifica inversamente.
Esquema de calificación:

Instrucciones de presentación:
- Cargada de lienzo
- Un informe bien formateado que cubre las estructuras de datos elegidas, el análisis de complejidad, los resultados y el código.
- Cargar código de programa para la ejecución. Asegúrese de proporcionar ReadMe para TA.
- Además, la copia impresa del informe sin código para mí en la clase.
Proyecto 2: Algoritmos gráficos (ruta más corta de la fuente de solteros y árbol de expansión mínimo)
En este proyecto, implementará dos algoritmos gráficos mencionados a continuación. Nota: Puede trabajar solo o en un equipo de dos máximos.
Problema 1: Encuentre el árbol de ruta más corto en gráficos ponderados dirigidos y no dirigidos para un vértice de origen dado. Suponga que no hay un borde negativo en su gráfico. Imprimirá cada costo de ruta y ruta para una fuente determinada.
Problema 2: Dado un gráfico conectado, no dirigido y ponderado, encuentre un árbol de expansión usando bordes que minimice el peso total? (?) = ∑ (u, v) ∈T ? (?,?). Use el algoritmo Kruskal para encontrar un árbol de expansión mínimo (MST). Imprimirá los bordes del árbol y el costo total de su respuesta.
Formato de entrada: para cada problema, tomará la entrada de un archivo de texto. Digamos que desea ejecutar algoritmo en el siguiente gráfico no dirigido. El formato de archivo correspondiente sería:
6 10 U
A B 1
A C 2
B C 1
B D 3
B E 2
C D 1
C E 2
D E 4
D F 3
E F 3
A
Aquí, los dos primeros números representan el número de vértices y bordes. La letra U representa el gráfico no dirigido (D para dirigido). Desde la segunda línea, menciona todos los bordes y su peso (¡por ejemplo, ???? (?,?) Y su peso es 1. La última línea es opcional. Si se da, representa el nodo fuente.
Instrucciones de presentación:
- Un informe bien formateado que cubre una breve descripción de cada algoritmo, estructura de datos elegida, tiempo de ejecución de su código, entrada/salida de muestra, instrucción para ejecutar su programa fácilmente.
- Para cada problema, ejecute su programa para cuatro gráficos diferentes de su elección. Use su juicio para definir los gráficos de prueba que cree interesantes y razonables. Por ejemplo:
- Gráfico no dirigido: al menos 7 nodos y 12 bordes
- Gráfico dirigido: al menos 7 nodos y 15 bordes
- Código limpio para que TA ejecute.
- Puede usar cualquier lenguaje de programación (por ejemplo, C/C ++, Java, Python, etc.)
- Si se trabaja en un equipo, ambos miembros deben enviar todo por separado.
- Copia impresa de su informe directamente; una copia por equipo.
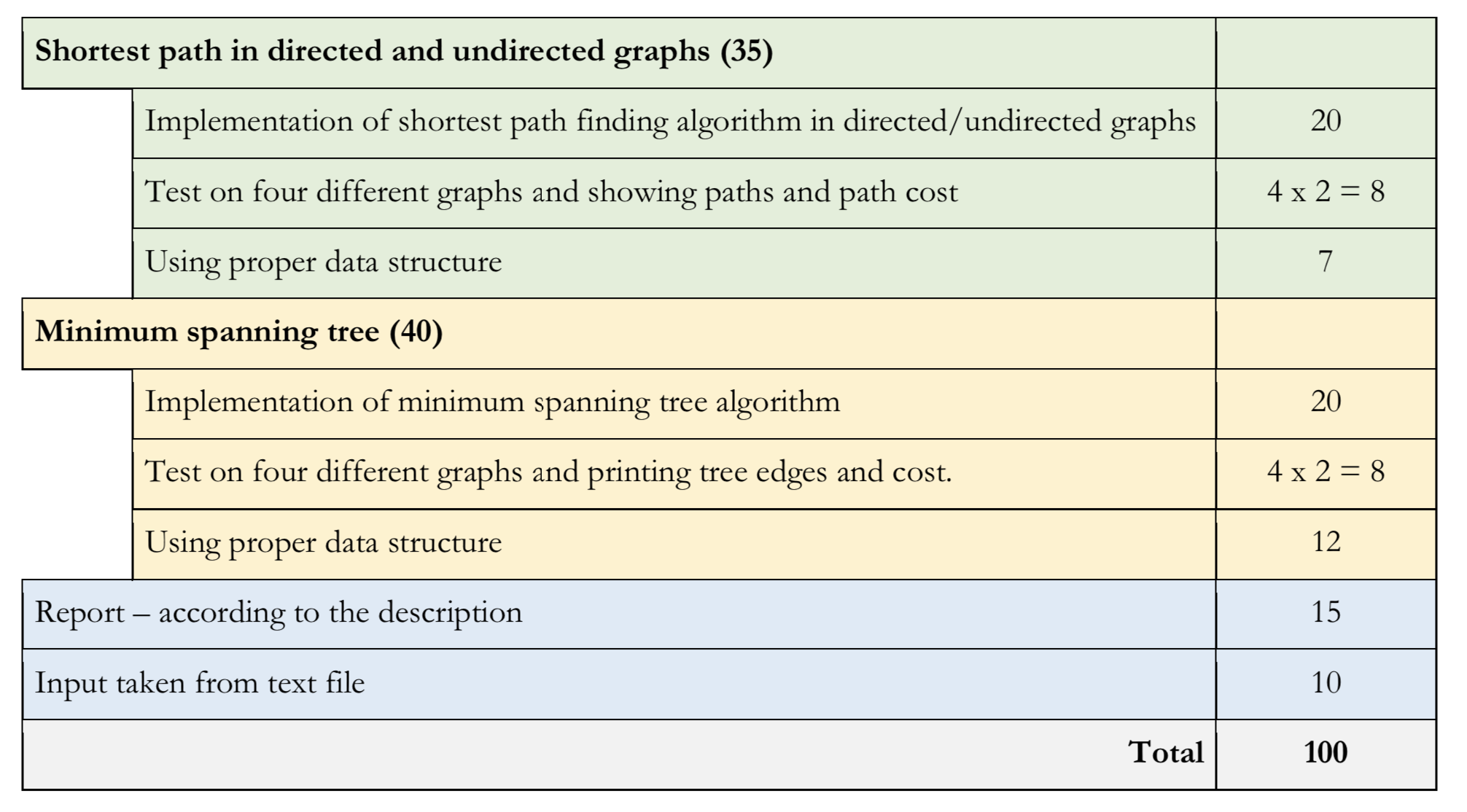
Esquema de calificación:
Proyecto 3: Algoritmos de coincidencia de patrones
Nota: Puede trabajar solo o en un equipo de tres máximos.
Para esta tarea, implementará solo tres algoritmos de coincidencia de patrones de su elección de la lista que se proporciona a continuación.
- Algoritmo de fuerza bruta
- Algoritmo de Boyer-Moore-Horspool
- Algoritmo Knuth-Morris-Pratt
- Algoritmo de Boyer-Moore
- Automatización finita para la coincidencia de patrones
Experimento:
- Compare tres algoritmos para varios textos y patrones de entrada diferentes; al menos 10 casos diferentes
- Mencione el número de comparaciones requeridas en una tabla para cada caso, para cada algoritmo
Envío:
- Un informe bien formateado que cubre una breve descripción de cada algoritmo, estructura de datos utilizada, tiempo de ejecución de su código, entrada/salida de muestra, instrucción para ejecutar su programa fácilmente.
- Código limpio para que TA ejecute.
- Puede usar cualquier lenguaje de programación (por ejemplo, C/C ++, Java, Python, etc.)
- Si se trabaja en un equipo, aún se requiere que ambos miembros envíen todo por separado.
- Hardcopy de su informe directamente; una copia por equipo.
Esquema de calificación:
- 3 x 15 = 45 puntos: para implementar tres algoritmos
- 20 puntos: para el experimento
- 10 puntos: informe

