Algorithm A*
On
? How to know if a possibility is promising?
- Through the function f (x) = g (x) + h (x)
- Which is a heuristic function
- g (x) is the cost to, from origin, reach the x node
- h (x) is a heuristic function for estimating the cost of the next node
- We always look at the possibilities of expanding the tree and calculate the value of f (x)
- We add the node that has the smallest f (x) among those we find
- OA* is the most efficient algorithm for minimum ways in graphs
- However, it severe limitations
- It is necessary to define a h (x) that is admissible: it will never return a value greater than the actual distance from x to y
- If h (x) is admissible, but too underestimated the actual distance, the algorithm is super inefficient. If h (x) is not admissible, the algorithm may not find the minimum way
? Complexity
- Complexity depends directly on the function H (x) used.
- In the worst case, the amount of nodes explored is exponential in the size of the smallest path, but has polynomial complexity if H ∗ (x) −H (x) ≤O (Logh ∗ (x)).
? When is it good to use?
- Graphs where one can underestimate the distance between two vertices, as in maps
- The shortest distance between two points is a line, but probably the actual distance will be greater than that
? What is the minimum way in this case?
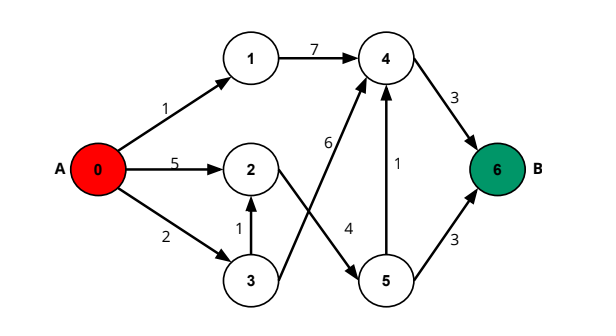
Execute the project
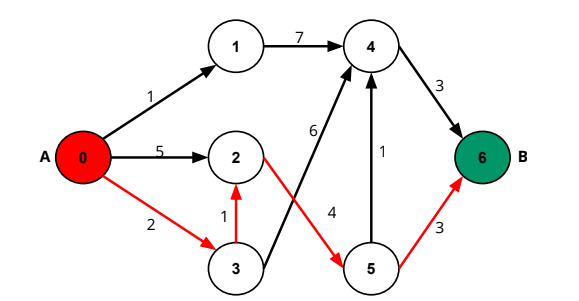
Result
authors
License
This project is under the MIT. See here for more information.


