Write programs to implement IEEE 802.3 Ethernet frame encapsulation.
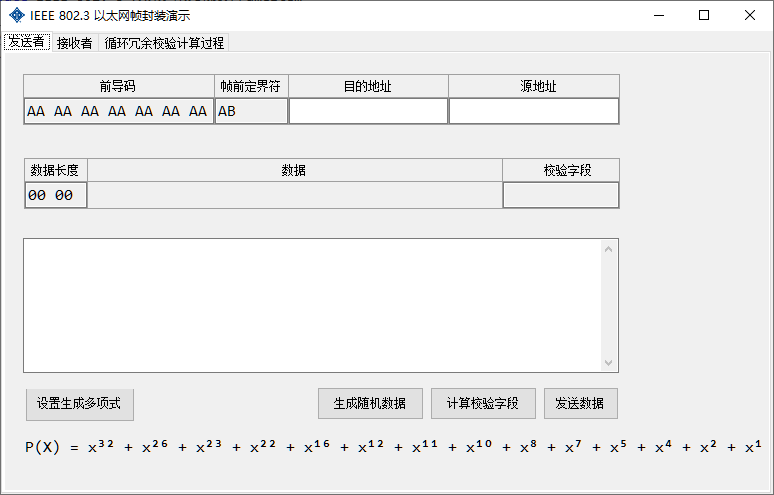
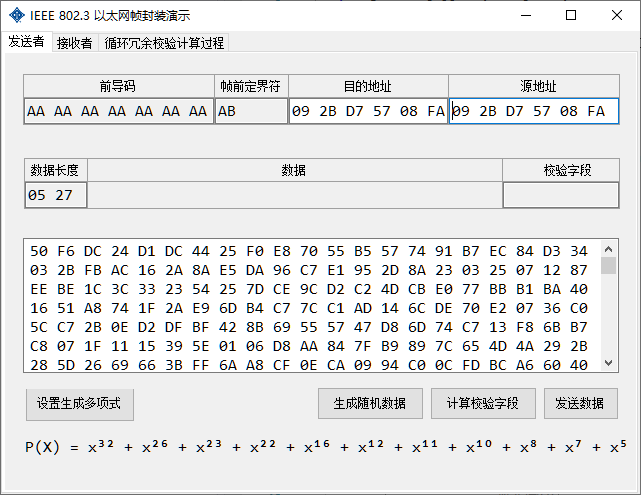
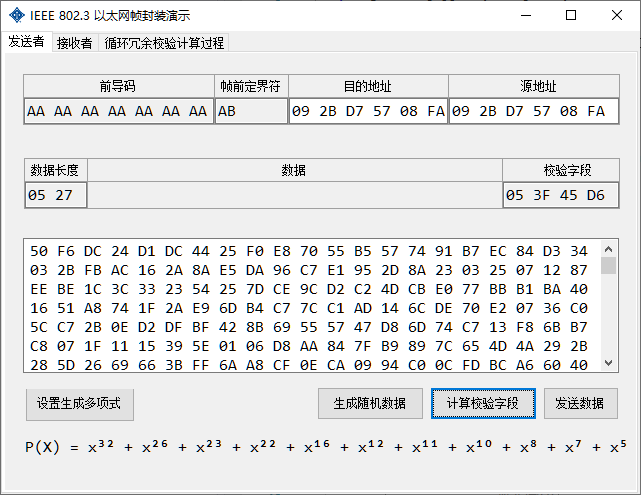
It is required to draw the interface, and the data part, source MAC address and destination MAC address of the Ethernet frame are input from the interface;
The calculated checksum field and the encapsulated result can be output from the interface;
Generate polynomial G(X)=X8+X2+X+1;
The operating system, language and compilation environment used are not limited, but must be noted in the report.
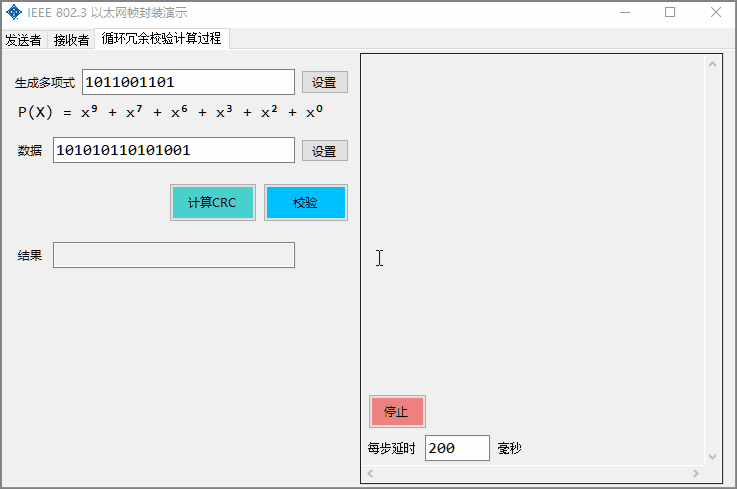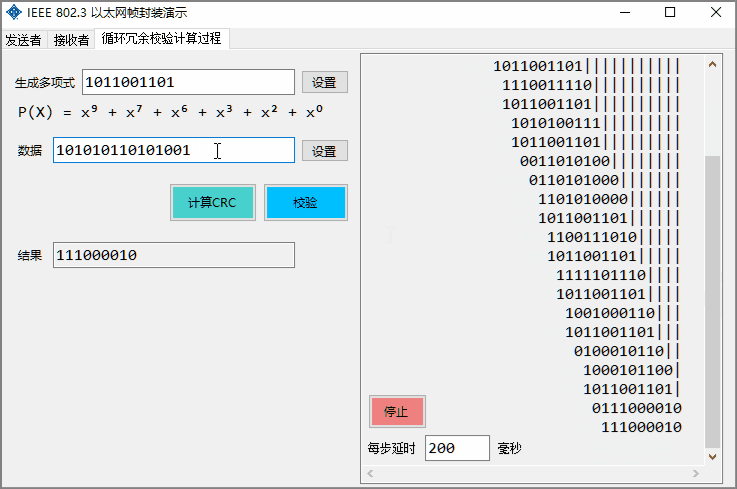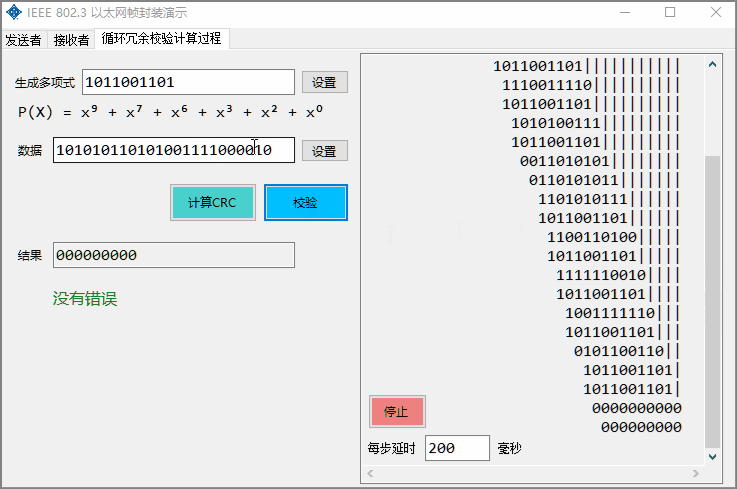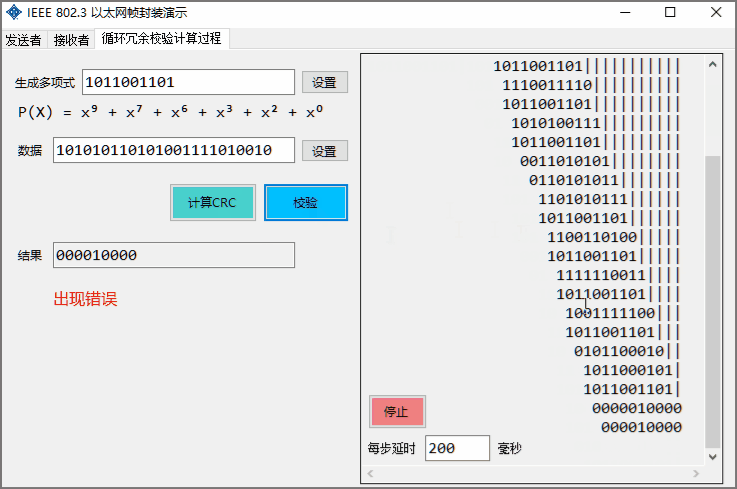
Able to visualize the CRC calculation process;
Ability to control the operation of the program from the interface.
The frame structure according to the 802.3 standard is shown in the following table (the Ethernet frame structure of the 802.3 standard consists of 7 parts)
802.3 standard frame structure
| Lead code | Pre-frame delimiter | Destination address | Source address | Length field | Data fields | Verification field |
|---|---|---|---|---|---|---|
| 7B | 1B | (6B) | (6B) | (2B) | (Variable length) | (4B) |
Among them, the minimum length of the frame data field is 46B. If the frame has less than 46B, the data field should be filled to 46B. The padding character is arbitrary and does not count to the length field value.
In the check field, CRC check is used. The scope of verification includes the destination address field, the source address field, the length field, and the LLC data field.
Use a visual interface to receive the destination address, source address, length field, and data field entered by the user. It also supports the generation of random data, which can reduce user input
Use the generated polynomial to calculate the verification field of the data to be checked. The field to be checked is an integer byte, the order of the polynomial generated does not exceed 32, and the calculated remainder is 4 bytes.
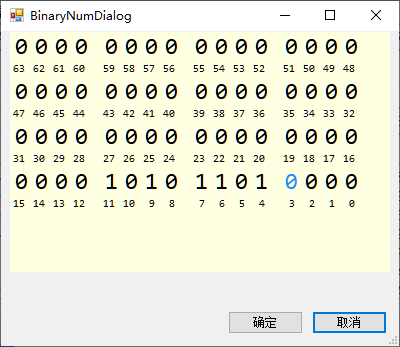
Imitating the bit input keyboard of Windows 10 calculator, allowing users to input and generate polynomials and other data by clicking the mouse
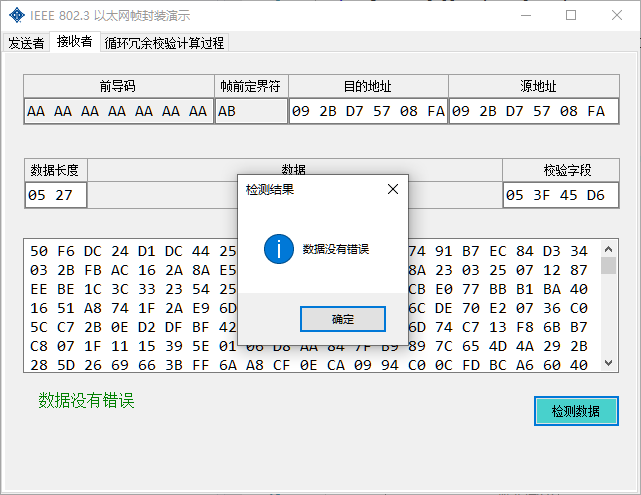
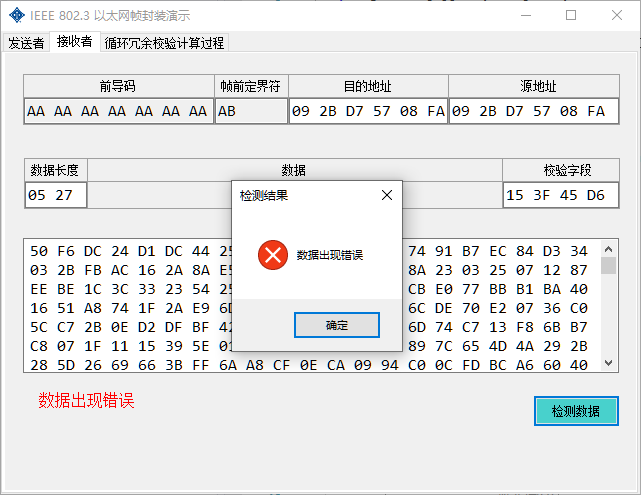
The frame after the calculation of FCS occurs to the receiver, and the receiver can verify whether there is an error. You can simulate errors, such as manually modifying the data and then verifying whether there is an error.
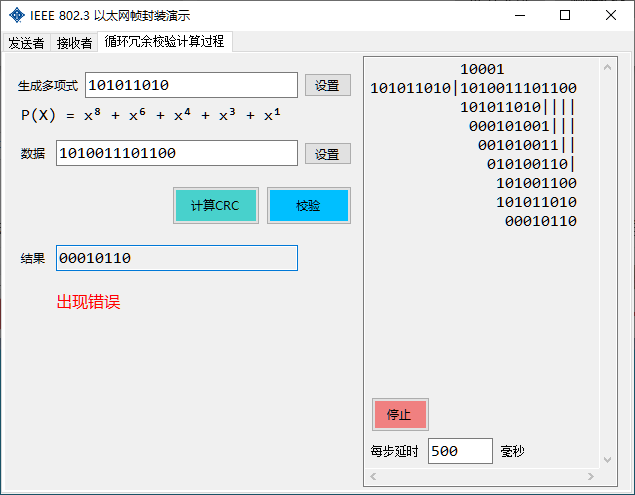
Using shorter binary data, dynamically display the CRC calculation process and support verification function. The delay time of each step can be customized to control the display speed and the presentation can be stopped at any time.
According to the following formula
Can get
That is, expand a number n times, and then add the remainder. At this time, the remainder of $$mod m$$ remains unchanged
private byte [ ] CalcCRC ( string v )
{
var data = new Queue < char > ( v . ToArray ( ) ) ; // 被除数
char [ ] divisor = binaryString . ToArray ( ) ; // 除数
Queue < char > S = new Queue < char > ( ) ; // 商
int width = divisor . Length ; // 每次取 width 个字符进行异或运算
Queue < char > str = new Queue < char > ( ) ; // 每次取的长度为 width 的部分被除数
// 获取前 width - 1 个字符,填入到str中
for ( int i = 0 ; i < width - 1 ; i ++ )
{
str . Enqueue ( data . Dequeue ( ) ) ;
}
while ( data . Count != 0 )
{
str . Enqueue ( data . Dequeue ( ) ) ;
if ( str . First ( ) == '0' )
{
S . Enqueue ( '0' ) ;
str . Dequeue ( ) ;
}
else
{
S . Enqueue ( '1' ) ;
var temp = str . ToArray ( ) ;
str . Clear ( ) ;
for ( int i = 1 ; i < temp . Length ; i ++ )
{
str . Enqueue ( temp [ i ] == divisor [ i ] ? '0' : '1' ) ;
}
}
}
// 计算已经结束,str中的值就是结果,下面的代码可以不用看了
// 将str中的值转成4个字节的二进制数组
var res = new string ( str . ToArray ( ) ) . PadLeft ( 32 , '0' ) ;
var result = new byte [ 4 ] ;
// 将字符串格式化为byte
for ( int i = 0 ; i < 4 ; i ++ )
{
result [ i ] = Convert . ToByte ( res . Substring ( i * 8 , 8 ) , 2 ) ;
}
return result ;
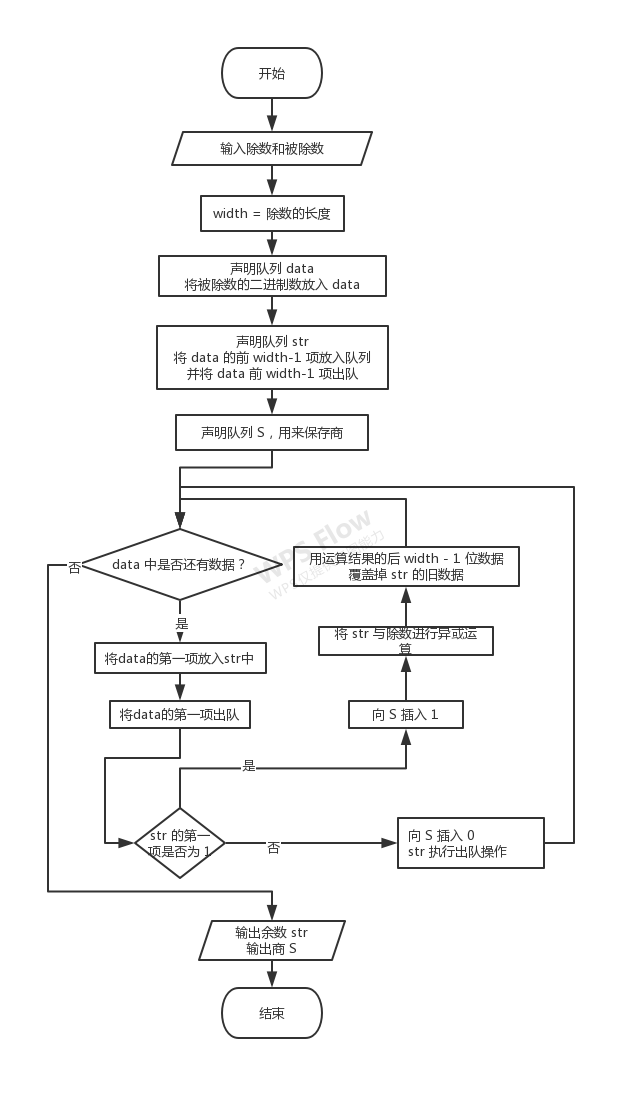
}Pending data: 1010 0111 0110 0
Generate polynomial: 1010 1101 0 (
Put all pending data into queue data
data = [1010011101100]
Generate a polynomial of 9 bits, so first let the first 8 items of the queue data be dequeued and put the data into the queue str
str = [10100111]
data = [01100]
Queue data.Count = 5 != 0, continue execution
Dequeue the first item of the queue data and put it into the queue str
str = [101001110]
data = [1100]
The first element of str is 1
Insert 1 into the column S
Perform bitwise exclusive OR of the value of the queue str and the value of the generated polynomial, and copy the last 8 characters of the result to str 101001110 ^ 10101101010 = 000010100
S = [1]
str = [00010100]
data = [1100]
Queue data.Count = 4 != 0, continue execution
Dequeue the first item of the queue data and put it into the queue str
S = [1]
str = [000101001]
data = [100]
The first element of str is 0
Insert 0 into column S and let str 's first item dequeue
S = [10]
str = [00101001]
data = [100]
Queue data.Count = 3 != 0, continue execution
Dequeue the first item of the queue data and put it into the queue str
S = [10]
str = [001010011]
data = [00]
The first element of str is 0
Insert 0 into column S and let str 's first item dequeue
S = [100]
str = [01010011]
data = [00]
Queue data.Count = 2 != 0, continue execution
Dequeue the first item of the queue data and put it into the queue str
S = [100]
str = [010100110]
data = [0]
The first element of str is 0
Insert 0 into column S and let str 's first item dequeue
S = [1000]
str = [10100110]
data = [0]
Queue data.Count = 1 != 0, continue execution
Dequeue the first item of the queue data and put it into the queue str
S = [1000]
str = [101001100]
data = []
The first element of str is 1
Insert 1 into the column S
Perform bitwise exclusive OR of the value of the queue str and the value of the generated polynomial, and copy the last 8 characters of the result to str 101001100 ^ 10101101010 = 000010110
S = [10001]
str = [00010110]
data = []
Queue data.Count = 0 == 0, end, remainder is str = 00010110 , quotient is S = 10001
The entire calculation process is: