Dieser Artikel vermittelt Ihnen relevantes Wissen über JavaScript und stellt hauptsächlich den relevanten Inhalt zu Zahlentypen vor. Es gibt zwei Arten von Zahlen in JavaScript: Ich hoffe, dass sie für Sie nützlich sind. helfen.
[Verwandte Empfehlungen: Javascript-Video-Tutorial, Web-Frontend]
In JavaScript gibt es zwei Arten von Zahlen:
Der Number , bei dem es sich um einen Zahlentyp im herkömmlichen Sinne handelt, wird im 64 Bit- IEEE-754 -Format gespeichert und ist eine „Gleitkommazahl mit doppelter Genauigkeit“. Bisher sind es alle Zahlen, mit denen wir in Berührung gekommen sind vom Typ Number ;
Der Typ BigInt repräsentiert ganze Zahlen beliebiger Länge, es sei denn, sie stellen andere Zahlen als 2 53 bis -2 53 dar. Wir werden diese professionellen Datentypen in späteren Kapiteln ausführlich vorstellen;
Die Art und Weise, Zahlen zu schreiben, ist sehr einfach, aber JavaScrpt verfügt über viele praktische und schnelle syntaktische Zucker, die wir verwenden können. Das Erlernen dieser syntaktischen Zucker verbessert nicht nur unsere Fähigkeit, Code zu lesen, sondern verbessert auch den Sinn unseres Codes auf hoher Ebene.
Dezimalzahlen sind am einfachsten und wir werden sie in fast jedem Artikel verwenden. Beispielsweise erstellen wir eine Variable und speichern 100 Milliarden:
seien zehn Milliarden = 10000000000;
Obwohl die Operation sehr einfach ist, gibt es ein Problem: Es ist schwierig zu zählen, wie viele 0 auf 1 folgen. Wenn wir einen Überweisungscode schreiben, kann eine falsche 0 zum Bankrott führen.
Zu diesem Zeitpunkt können wir _ wie folgt als Trennzeichen verwenden:
let tenbillion = 10_000_000_000;
Der obige Code kann die Anzahl der 0 eindeutig zählen, was offensichtlich die optimale Lösung ist!
_ Unterstrich hier ist ein syntaktischer Zucker von JavaScript , der von der Engine während der Ausführung ignoriert wird. Die beiden oben genannten Schreibmethoden haben den gleichen Effekt, aber das Leseerlebnis ist sehr unterschiedlich.
Qingqi-Gehirnschaltkreis
Bei manchen Kinderschuhen muss man sich fragen, ich habe seit meiner Kindheit immer 4 0 Gruppen eingeteilt, warum muss ich 3 0 Gruppen bilden? Daher können wir es problemlos wie folgt schreiben:
let tenbillion = 100_0000_0000;
Oder es könnte so geschrieben werden:
let tenbillion = 1_0000_0000_00;
Was ich hier zum Ausdruck bringen möchte, ist, dass es keinen Einfluss auf die Größe der Zahl selbst hat, egal welche Divisionsmethode Sie verwenden. Überlegen Sie sich die leistungsstärkste Methode!
Obwohl die Verwendung _ viele 0 elegant teilen kann, schreiben wir es im wirklichen Leben im Allgemeinen nicht auf diese Weise. Beispielsweise schreiben wir 10000000000 oft als „10 Milliarden“, sodass viele 0 weggelassen werden können, wodurch die Wahrscheinlichkeit einer Bildung verringert wird Fehler.
JavaScript bietet auch eine Möglichkeit, 0 wegzulassen. Wir können den Buchstaben e gefolgt von einer Zahl verwenden, um die Zahl 0 darzustellen. Beispiel:
let tenbillion = 1e10;//10 billion, 1 gefolgt von 10 0sconsole.log(3.14e9);//3140000000, gefolgt von 7 0s, schauen Sie bitte nach unten, wenn Sie Fragen haben.
Das Verständnis des obigen Codes ist sehr einfach. e10 kann als 1_0000_0000_00 verstanden werden 0 was 1 gefolgt von 10 ist. Wir können also denken:
1e10 === 1 * 1_0000_0000_00;//e10 bedeutet 1 gefolgt von 10 03.14e9 === 3.14 * 1_000_000_000;//e9 bedeutet 1 gefolgt von 9 Nullen
Wir können diese Methode auch verwenden, um sehr kleine Zahlen darzustellen, beispielsweise 1 Nanometer:
let nm = 0,000000001; //Einheit (Meter)
Da es zu viele 0 gibt, können wir auch _ verwenden:
sei nm = 0.000_000_001;
Natürlich können Sie e auch alle 0 weglassen, wie folgt:
let nm = 1e-9;//9 0s links von 1, einschließlich der vor dem Dezimalpunkt
Mit anderen Worten bedeutet e-9 1 -9 , also 1/1000_000_000 , sodass die folgende Gleichung wahr ist:
1e-9 === 1 / 1_000_000_000;3.14e-8 === 3.14 / 1_000_000_00;
Hexadezimal ist ein Format, das häufig in der Programmierung verwendet wird, z. B. für Farbe, Codierung usw. Wir können 0x vor gewöhnlichen Zahlen hinzufügen, um hexadezimale Zahlen darzustellen:
let hex = 0xff;//255, Groß-/Kleinschreibung nicht beachtet, 0xFF ist dasselbe
Binärzahlen beginnen mit 0b :
let bin = 0b1011;//11
Oktalzahlen beginnen mit 0o :
let oct = 0o777;//511
Diese einfache Schreibmethode unterstützt nur diese drei speziellen Typen. Für andere Basiszahlen können Sie spezielle Funktionen verwenden, um sie zu generieren ( parseInt ).
Die toString -Methode kann die Zahl in eine Zeichenfolgenform umwandeln, die base entspricht.
Schenken Sie eine Kastanie:
sei num = 996; console.log(num.toString(8));//In oktale Zeichenfolge konvertieren console.log(num.toString(16));//In hexadezimale Zeichenfolge konvertieren console.log(num.toString( 32));// Konvertieren Sie in eine 32-Hexadezimalzeichenfolge
Die Ergebnisse der Codeausführung lauten wie folgt:
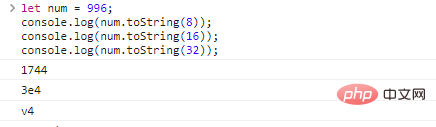
Der base kann zwischen 2 und 36 liegen. Wenn nichts ausgefüllt ist, ist der Standardwert 10 .
Beachten Sie, dass Sie in einigen Fällen zwei anwenden müssen . wenn Sie Zahlen verwenden, um die toString -Methode direkt aufzurufen, zum Beispiel:
console.log(123.toString(8));//Fehler, Syntaxfehler console.log(123..toString(8));//Richtig, 173
Es gibt zwei . nach der Zahl. Dies liegt daran, dass der erste . nach der Zahl als JavaScript betrachtet wird und der zweite Punkt der ist, der die Funktion aufruft .
Wenn es sich um eine Dezimalzahl handelt, besteht dieses Problem nicht. Beispiel:
console.log(3.14.toString(8));
Oder wir können Klammern verwenden, um die Verwendung von zwei Punkten zu vermeiden, zum Beispiel:
console.log((123).toString(8));//'173
Das Runden ist eine der gebräuchlichsten Operationen für Zahlen und umfasst normalerweise:
Abrunden, Math.floor(num)
console.log(Math.floor(3.14));//3 console.log(Math.floor(9.99));//9 console.log(Math.floor(-3.14));//-4 console.log(Math.floor(-9.99));//-10
Befolgen Sie nicht das Rundungsprinzip und nehmen Sie direkt die nächste ganze Zahl, die kleiner oder gleich dem aktuellen Wert ist.
Aufrunden, Math.ceil(num)
console.log(Math.ceil(3.14));//4 console.log(Math.ceil(9.99));//10 console.log(Math.ceil(-3.14));//-3 console.log(Math.ceil(-9.99));//-9
Befolgen Sie nicht das Rundungsprinzip und nehmen Sie direkt die nächste ganze Zahl, die größer oder gleich der aktuellen Zahl ist.
Auf die nächste ganze Zahl runden, Math.round(num)
console.log(Math.round(3.14));//3 console.log(Math.round(9.99));//10 console.log(Math.round(-3.14));//-3 console.log(Math.round(-9.99));//-10
Nach dem Rundungsprinzip wird die ganze Zahl genommen, die der aktuellen Zahl am nächsten kommt.
Dezimalstellen entfernen, Math.trunc(num)
console.log(Math.trunc(3.14));//3 console.log(Math.trunc(9.99));//9 console.log(Math.trunc(-3.14));//-3 console.log(Math.trunc(-9.99));//-9
Entfernen Sie direkt die Zahlen nach dem Komma und runden Sie sie auf ganze Zahlen. Der IE-Browser unterstützt diese Methode nicht
Vergleichen Sie die oben genannten vier Methoden:
| Mathe.Boden | Mathe.decke | Matherunde | Math.trunc | |
|---|---|---|---|---|
| 3.14 | 3 | 4 | 3 | 3 |
| 9,99 | 9 | 10 | 10 | 9 |
| -3.14 | -4 | -3 | -3 | -3 |
| -9,99 | -10 | -9 | -10 | -9 |
Die obige Methode rundet die Dezimalzahl einfach in eine ganze Zahl. In manchen Fällen benötigen wir Dezimalzahlen mit einer bestimmten Genauigkeit. Was sollen wir beispielsweise tun, wenn wir die letzten 4 Ziffern von Pi nehmen?
Es gibt zwei Methoden:
Mathe-Multiplikation und Divisionszählung
let pi = 3.1415926;console.log(Math.round(pi * 10000) / 10000);//3.1416
Der obige Code multipliziert zuerst pi mit 10000 , rundet ihn dann und dividiert ihn dann durch 10000 , um so ein Ergebnis zu erhalten, das den Genauigkeitsanforderungen entspricht. Dies scheint jedoch albern und JavaScript bietet uns einen einfacheren Weg.
toFixed(n)
sei pi = 3.1415926;console.log(pi.toFixed(4));//3.1416
Der obige Code scheint kein Problem mit der Ausgabe zu haben. Tatsächlich gibt toFixed einen String zurück. Wenn wir einen numerischen Typ benötigen, können wir ihn mit dem unären Operator + pi.toFixed(4) konvertieren.
Wenn die Dezimalmantisse außerdem nicht lang genug ist, fügt toFixed am Ende '0' hinzu:
let num = 3.1;console.log(num.toFixed(9));
Die Ergebnisse der Codeausführung lauten wie folgt: 
Dies beweist auch, dass der Rückgabewert von toFixed ein String ist, andernfalls wird 0 weggelassen.
Gleitkommadarstellungen sind in vielen Fällen immer voreingenommen
Im Computer werden Gleitkommazahlen gemäß IEEE-754 Standard dargestellt, wobei Gleitkommazahlen mit einfacher Genauigkeit 32 Bit und Gleitkommazahlen mit doppelter Genauigkeit 64 Bit betragen. Bei einer Gleitkommazahl mit doppelter Genauigkeit wird 1 Bit zur Darstellung des Vorzeichens, 52 Bit zur Speicherung der signifikanten Ziffern und 11 Bit zur Speicherung der Position des Dezimalpunkts verwendet.
Obwohl 64 Bit bereits sehr große Zahlen darstellen können, besteht immer noch die Möglichkeit, die Grenze zu überschreiten, zum Beispiel:
let bigNum = 1e999;console.log(bigNum);//Infinity
Die Zahl, die den Maximalwert überschreitet, wird zur Infinity (unendlich) und verliert somit die Größe der ursprünglichen Zahl, was eine Art Abweichung darstellt.
Es gibt noch eine andere Art von Abweichung, die wir lernen müssen:
console.log(0.1+0.2 === 0.3);//falseconsole.log(0.1 + 0.2);
Die Ergebnisse der Codeausführung lauten wie folgt:
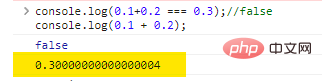
Das ist richtig, das Ergebnis von 0.1 + 0.2 ist nicht 0.3 , sondern eine Reihe von 0 gefolgt von einer 4 .
Diese Art der Abweichung ist sehr fatal, insbesondere in Einkaufszentren und Bankarbeitsszenarien. Selbst eine sehr kleine Abweichung führt in Szenarien mit hohem Umsatz zum Verlust endlosen Reichtums.
Ich habe einmal eine Geschichte über einen Bankangestellten gehört, der Millionen von Dollar gestohlen hat, indem er jedem Mitarbeiter den Lohn von nur 20 Cent abgezogen hat!
Ich denke, wenn mir das passieren würde, wäre ich definitiv nicht in der Lage, es zu finden, deshalb ist es so wichtig, immer genau zu sein.
Ich weiß nicht, ob diese Geschichte wahr ist oder nicht~~
Nehmen wir als Beispiel unser gemeinsames Dezimalsystem. Wir alle wissen, dass es bei Dezimalzahlen zwei seltsame Dinge gibt, eines heißt unendliche sich wiederholende Dezimalzahlen und das andere heißt unendliche sich nicht wiederholende Dezimalzahlen. Beispielsweise ist 1/3 eine unendliche Wiederholung dezimal 0.3333333(3) , und pi Es ist eine unendliche, sich nicht wiederholende Dezimalzahl. Unendlich bedeutet, dass die Größe der Zahl nicht eindeutig numerisch beschrieben werden kann und das, was wir schreiben können, ungenau ist.
Es gibt auch einige Endlosschleifenzahlen im Binärformat. Der Unterschied besteht darin, dass eine Zahl wie 0.1 die sehr einfach aussieht, im Binärformat eine Endlosschleifendezimalzahl ist.
Zum Beispiel:
let x = 0.1;console.log(x.toFixed(20));
Die Ergebnisse der Codeausführung lauten wie folgt:
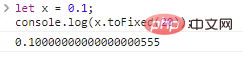
Finden Sie es nicht unglaublich? Wir haben einfach eine Variable erstellt und ihr den Wert 0.1 zugewiesen und dann 20 Dezimalstellen verwendet, aber wir haben ein unglaubliches Ergebnis erhalten.
Wenn wir den Winkel ändern, ist es möglicherweise einfacher, dieses Phänomen zu verstehen. Im Dezimalsystem ist jede durch 10 oder 10 ganze Potenzen geteilte ganze Zahl eine normale und genaue Zahl, beispielsweise 1/10 oder 996/1000 . Wenn Sie jedoch durch 3 dividieren, erhalten Sie ein Schleifenergebnis, z. B. 1/3 .
Diese Beschreibung gilt auch, wenn sie in eine Binärdatei konvertiert wird.
Im Binärsystem ist jede durch 2 geteilte ganze Zahl oder eine ganzzahlige Potenz von 2 eine normale exakte Zahl. Wenn Sie sie jedoch durch 10 teilen, erhalten Sie eine Endlosschleife von Binärzahlen.
Daraus können wir schließen, dass Binärzahlen 0.1 und 0.2 nicht genau darstellen können, genauso wie Dezimalzahlen 1/3 nicht beschreiben können.
Beachten:
Diese Art der Datenabweichung ist kein Fehler von JavaScript, sondern führt zum gleichen Ergebnis für PHP, Java, C, Perl und Ruby.
Rundung
Bei der Anzeige einer unendlich wiederkehrenden Dezimalzahl können wir die toFixed -Methode direkt verwenden, um die Dezimalzahl zu runden. Diese Methode gibt direkt eine Zeichenfolge zurück, was für die Preisanzeige sehr praktisch ist.
0.3.toFixed(2);//0.30
Verwenden Sie kleine Einheiten
Eine andere Möglichkeit besteht darin, kleinere Einheiten zur Berechnung von Preisen und Entfernungen zu verwenden, beispielsweise die Verwendung von Cent anstelle von Yuan, um den Gesamtpreis zu berechnen. Tatsächlich tun dies viele Handelswebsites. Diese Methode verringert jedoch nur die Häufigkeit des Auftretens von Dezimalstellen, und es gibt keine Möglichkeit, das Auftreten von Dezimalstellen vollständig zu vermeiden.
In JavaScript Zahlen gibt es zwei besondere Werte: Infinity und NaN .
Wie kann man beurteilen, ob eine Zahl eine normale Zahl ist?
Wir können zwei Methoden verwenden:
isFinite(val)
Diese Funktion konvertiert den Parameter val in einen numerischen Typ, bestimmt dann, ob die Zahl endlich ist, und gibt true zurück, wenn die Zahl nicht NaN , Infinity oder -Infinity ist.
console.log(isFinite(NaN));//falseconsole.log(isFinite(Infinity));//falseconsole.log(isFinite(3));//trueconsole.log(isFinite('12'));// WAHR Die Ergebnisse der Codeausführung lauten wie folgt: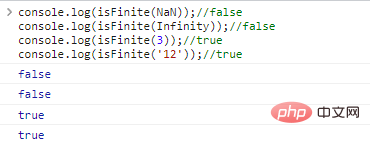
Da eine Zeichenfolge, die nicht in eine Zahl umgewandelt werden kann, in NaN umgewandelt wird, können wir die Methode isFinite verwenden, um zu bestimmen, ob die Zeichenfolge eine numerische Zeichenfolge ist:
console.log(isFinite('xxxx'));//falseconsole.log(isFinite('Infinite'));//falseconsole.log(isFinite(' '));//true, leere Zeichenfolge wird in 0 konvertiertDie Ergebnisse der Codeausführung lauten wie folgt:
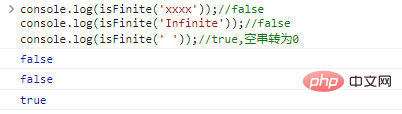
isNaN(Wert)
Gibt true zurück, wenn val NaN oder ein anderer Wert ist, der nicht in eine Zahl umgewandelt werden kann.
console.log(isNaN(NaN));//trueconsole.log(isNaN('Infinite'));//true Ergebnisse der Codeausführung: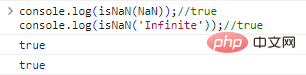
Warum die Funktion isNaN verwenden, anstatt sie direkt zu lesen?
Zum Beispiel:
console.log(NaN === NaN);//false
Die Ergebnisse der Codeausführung lauten wie folgt:
Dies liegt daran, dass NaN keiner Zahl entspricht, auch nicht sich selbst.
Object.is(a,b) kann bestimmen, ob die Parameter a und b gleich sind. Wenn sie gleich sind, gibt es true zurück, andernfalls gibt es false zurück. Die Ergebnisse haben nur drei Situationen:
Kann mit NaN verglichen werden
console.log(Object.is(NaN,NaN));//true
Ergebnisse der Codeausführung:

0 und -0
console.log(Object.is(0,-0));//false
Ergebnisse der Codeausführung:

Im Computer werden Positiv und Negativ durch 0 und 1 dargestellt. Aufgrund unterschiedlicher Vorzeichen sind 0 und -0 tatsächlich unterschiedlich und werden auf unterschiedliche Weise ausgedrückt.
andere
Andere Vergleichssituationen sind genau die gleichen wie a === b .
Im Gegensatz zu + und Number können parseInt und parseFloat Zeichenfolgen in Zahlen umwandeln. Wenn Sie beispielsweise + und Number für eine Zeichenfolge wie "100¥" verwenden, wird zwangsläufig NaN zurückgegeben, aber parseInt und parseFloat können damit problemlos umgehen.
Zum Beispiel:
console.log(+"100¥");console.log(parseInt("100¥"));console.log(parseFloat("12.5¥"));Ergebnisse der Codeausführung:
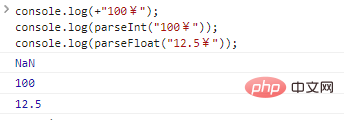
parseInt und parseFloat lesen Zahlen aus einem String, bis sie nicht mehr gelesen werden können. Beide eignen sich besonders für die Verarbeitung von Zeichenfolgen, die mit Zahlen wie "99px" und "11.4em" beginnen. Für Zeichenfolgen, die mit anderen Zeichen beginnen, wird jedoch NaN zurückgegeben.
console.log(parseInt('ff2000'));//NaN Wir haben jedoch festgestellt, ff2000 tatsächlich eine hexadezimale digitale Zeichenfolge ist. parseInt kann diese Situation ebenfalls bewältigen, muss jedoch einen hexadezimalen Parameter hinzufügen.
Zum Beispiel:
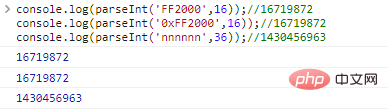
console.log(parseInt('FF2000',16));
//16719872
console.log(parseInt('0xFF2000',16));
//16719872
console.log(parseInt('nnnnnn',36));
//1430456963Ergebnisse der Codeausführung:
Das integrierte Math Objekt enthält viele Konstanten und Methoden, die wir häufig verwenden. Hier sind nur einige Beispiele für häufig verwendete:
Mathe.PI
Pi Π ist eine unendliche nichtzyklische Konstante, wir können stattdessen Math.PI verwenden:
console.log(Math.PI);

Math.random()
Generieren Sie eine Zufallszahl im Intervall [0,1) :
console.log(Math.random());console.log(Math.random());
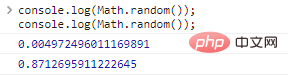
Wenn wir eine Zufallszahl innerhalb eines bestimmten Bereichs benötigen, können wir diese mit einem bestimmten Wert multiplizieren und dann runden.
Math.pow(a,b)
Berechnen Sie a b , zum Beispiel:
console.log(Math.pow(2,3));//8
Math.max()/Math.min()
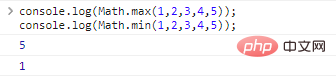
Wählen Sie aus einer beliebigen Anzahl von Argumenten einen Maximal-/Minimalwert aus:
console.log(Math.max(1,2,3,4,5));//5console.log(Math.min(1,2,3,4,5));//1